To find the true velocity of wind from relative velocity

[gnits]

Homework Statement

To find the true winde velocity from the relative wind velocity

Relevant Equations

Vr = Va - Vb

Please can I ask for help with the following as to where I'm going wrong.

Book answer is 20 knots and 315 degrees

My solution:

In the below diagram I have sketched the two situations, k is the true speed of the wind.

First question is, is my diagram correct?

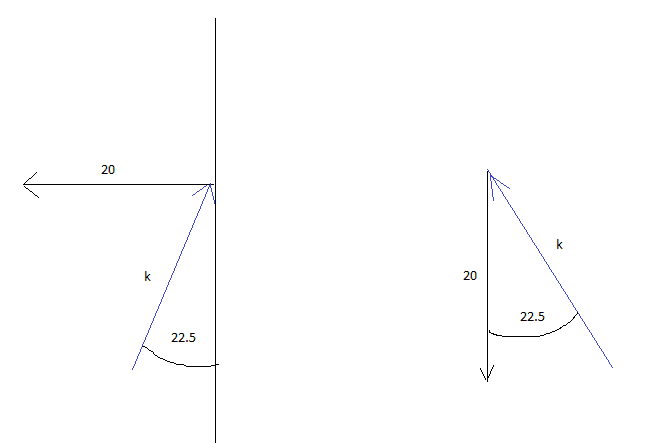
The velocity of the wind relaive to the ship $V_{ws}$ is given by:

$V_{ws}=V_w - V_s$

Where $V_w$ is the true velocity of the wind and $V_s$ is the true velocity of the ship.

Let i and j be unit vectors in the directions of east and north respectively
So in the two situations I have:

$k\,sin(22.5)i + k\,cos(22.5)j=V_{w_x}i+V_{w_y}j+20i$

and

$-k\,sin(22.5)i+k\,cos(22.5)j=V_{w_x}i+V_{w_y}j+20j$

Equating coefficients of i and j and solving for $V_{w_x}$ I get:

$V_{w_x}=-10$

and so:

$k=\frac{10}{sin(22.5)}=26.13$

and therefore

$V_{w_y}$=26.13*cos(22.5)=24.13

Which leads to a speed of 26.13 which is not the books answer.

Thanks,
Mitch.

 

[Cutter Ketch]

If you add the two equations, your two component equations pop out with very little algebra. Shouldn’t your last equation be

$V_{w_y} = 26.13*cos(22.5) - 10$ ?

Still not the book answer. Everything you did down to there looks right to me

 

[Cutter Ketch]

Actually, I take that back. That correction DOES give the book answer ... to the proper number of significant figures! It’s annoying because you and I know that in the real world that “0” in the ship’s speed just HAS to be significant. But, if the problem doesn’t explicitly say so ...

 

[gnits]

How did you get Vwy=26.13*cos(22.5)-10 ?
If I compare the coefficients of j in my two component equations do I not get:
k*cos(22.5)=Vwy AND k*cos(22.5)=Vwy+20
Which leads to Vwy=Vwy+20 which has no solution?

 

[haruspex]

$k\,sin(22.5)i + k\,cos(22.5)j=V_{w_x}i+V_{w_y}j+20i$
and
$-k\,sin(22.5)i+k\,cos(22.5)j=V_{w_x}i+V_{w_y}j+20j$

That appears to be four scalar equations but only three scalar unknowns. Can you spot your error from that?

 

[SammyS]

My solution:

In the below diagram I have sketched the two situations, k is the true speed of the wind.

First question is, is my diagram correct?

View attachment 260294

The velocity of the wind relative to the ship $V_{ws}$ is given by:

$V_{ws}=V_w - V_s$

Where $V_w$ is the true velocity of the wind and $V_s$ is the true velocity of the ship.
...

Thanks,
Mitch.

No, your diagram is not correct.

It's the relative velocity of the wind which is at an angle of ±22.5° . The magnitude of the relative velocity likely is different for the two situations.

Rearrange your equation and make the corresponding sketch.

$\vec {V}_{w}=\vec V_s + \vec V_{ws}$

 

[gnits]

Thanks all for your help, I see now that my original mistake was in the initial diagram. Indeed the speed is not the same in both cases. Have now solved and agree with book.

 

[SammyS]

Thanks all for your help, I see now that my original mistake was in the initial diagram. Indeed the speed is not the same in both cases. Have now solved and agree with book.

Thanks for letting us know that you solved the problem. Homework Helpers here at PF are volunteers. Our only reward is knowing that you have been helped, so, yes it's good that you indicted that you have a solution.

However, it's customary to post your solution. That will bring the thread to a nice conclusion and allow others to learn from this exercise.

 

[gnits]

I rewrote the original equations but with a different variable to represent each of the different speeds of the two realtive winds: $k_1\,sin(22.5)i + k_1\,cos(22.5)j=V_{w_x}i+V_{w_y}j+20i$ $-k_2\,sin(22.5)i+k_2\,cos(22.5)j=V_{w_x}i+V_{w_y}j+20j$ Now there are four equations and four unknowns: $k_1, k_2, V_{w_x}\,and\,V_{w_y}$ Solving for the latter two gives the book's answer. I made use of the half angle formula for tan to derive an exact value of $tan(22.5^{\circ})\,=\,\sqrt{2}-1$