gnits
- 137
- 46
- Homework Statement
- To find the weight of a hemisphere
- Relevant Equations
- moments
Could I please ask for help with the following question:
A uniform lamina of weight W is in the shape of a triangle ABC with AB = AC = 2a and the angle BAC equal to 2ᾳ. The side AB is fixed along a diameter of a uniform solid hemisphere of radius a. The plane of the lamina being perpendicular to the flat surface of the hemisphere. The body rests in equilibrium with a point on the curved surface of the hemisphere in contact with a horizontal table and with BC vertical. Show that the weight of the hemisphere is (8/9)*W cos(ᾳ)
Here's a diagram of the object with the flat surface of the hemisphere horizontal, and I've set up cartesian axes as shown:
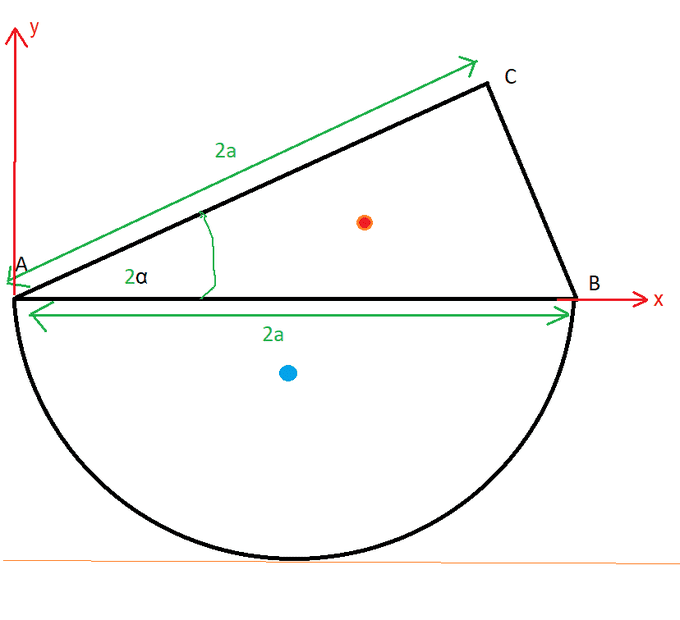
The orange dot represents the centre of gravity of the triangle and the blue dot that of the hemisphere.
Let the weight of the hemisphere be W_h
So:
A is the point (0,0)
B is the point (2a,0)
C is the point ( 2a*cos(2ᾳ) , 2a*sin(2ᾳ) )
I can use the standard results for the centre of mass of a triangle and a hemisphere, so:
centre of mass of hemisphere is at (a,-3a/8)
centre of mass of triangle is at ( (2a + 2a*cos(2ᾳ)) / 3, 2a*sin(2ᾳ) / 3 )
If I say that the centre of gravity of the whole body is at (x_bar, y_bar) then taking moments about x_bar I can say:
W * ((2a + 2a*cos(2ᾳ)) / 3 - x_bar) = -W_h *(x_bar - a),
This would give me W_h in terms of a, W and ᾳ but also x_bar.
I could find x_bar by equating moments of the triangle, hemisphere and composite body about the y-axis, this starts to get complicated.
Can anyone help me see the way forward?
Thanks,
Mitch.
A uniform lamina of weight W is in the shape of a triangle ABC with AB = AC = 2a and the angle BAC equal to 2ᾳ. The side AB is fixed along a diameter of a uniform solid hemisphere of radius a. The plane of the lamina being perpendicular to the flat surface of the hemisphere. The body rests in equilibrium with a point on the curved surface of the hemisphere in contact with a horizontal table and with BC vertical. Show that the weight of the hemisphere is (8/9)*W cos(ᾳ)
Here's a diagram of the object with the flat surface of the hemisphere horizontal, and I've set up cartesian axes as shown:
The orange dot represents the centre of gravity of the triangle and the blue dot that of the hemisphere.
Let the weight of the hemisphere be W_h
So:
A is the point (0,0)
B is the point (2a,0)
C is the point ( 2a*cos(2ᾳ) , 2a*sin(2ᾳ) )
I can use the standard results for the centre of mass of a triangle and a hemisphere, so:
centre of mass of hemisphere is at (a,-3a/8)
centre of mass of triangle is at ( (2a + 2a*cos(2ᾳ)) / 3, 2a*sin(2ᾳ) / 3 )
If I say that the centre of gravity of the whole body is at (x_bar, y_bar) then taking moments about x_bar I can say:
W * ((2a + 2a*cos(2ᾳ)) / 3 - x_bar) = -W_h *(x_bar - a),
This would give me W_h in terms of a, W and ᾳ but also x_bar.
I could find x_bar by equating moments of the triangle, hemisphere and composite body about the y-axis, this starts to get complicated.
Can anyone help me see the way forward?
Thanks,
Mitch.