gnits
- 137
- 46
- Homework Statement
- To locate the centre of gravity of a rod
- Relevant Equations
- moments
Could I please ask for a help on how to attack this question?
A heavy rod AB of length L can be made to balance across a small smooth peg C when a weight of 2W is suspended from A. Alternatively, it can be made to balance across the peg with a weight of 3W suspended from B. If the distance AC in the first case is the same as the distance BC in the second, show that the distance of the centre of gravity of the rod from A lies between (2/5)L and (1/2)L.
Here is my diagram for the two cases.
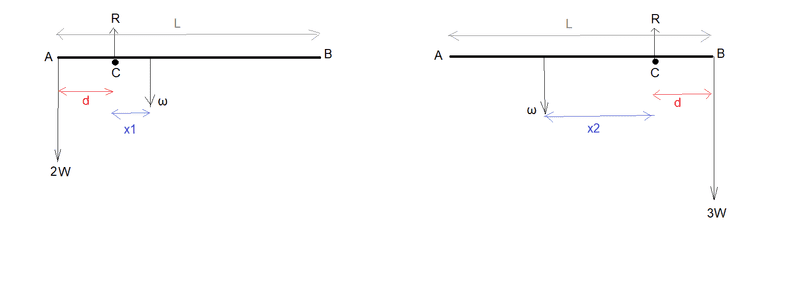
(I have called the weight of the rod ω)
In each diagram I have labelled ω as acting at the same point, but not at the centre point of AB, as I take it from this question that the rod is not of uniform density.
Well, if I take moments about C in the first case I get:
2Wd=ω*x1 giving x1 = 2Wd/ω
So the distance of the centre of gravity of the rod from A is:
d + x1 = d + 2Wd/ω.
Well, I can do the same for the second case giving distance of centre of gravity of the rod from A as:
L - d - x2 = L - d - 3Wd/ω
But I don't seem to be heading anywhere helpful!
Thanks for any pointer towards a solution,
Mitch.
A heavy rod AB of length L can be made to balance across a small smooth peg C when a weight of 2W is suspended from A. Alternatively, it can be made to balance across the peg with a weight of 3W suspended from B. If the distance AC in the first case is the same as the distance BC in the second, show that the distance of the centre of gravity of the rod from A lies between (2/5)L and (1/2)L.
Here is my diagram for the two cases.
(I have called the weight of the rod ω)
In each diagram I have labelled ω as acting at the same point, but not at the centre point of AB, as I take it from this question that the rod is not of uniform density.
Well, if I take moments about C in the first case I get:
2Wd=ω*x1 giving x1 = 2Wd/ω
So the distance of the centre of gravity of the rod from A is:
d + x1 = d + 2Wd/ω.
Well, I can do the same for the second case giving distance of centre of gravity of the rod from A as:
L - d - x2 = L - d - 3Wd/ω
But I don't seem to be heading anywhere helpful!
Thanks for any pointer towards a solution,
Mitch.