- #1
rudransh verma
Gold Member
- 1,067
- 96
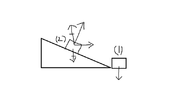
- Homework Statement
- A block of mass m is pushed towards a movable wedge of mass ##\eta m## and height h, with a velocity u. All surfaces are smooth. The minimum u for which the block will reach the top of the wedge is
- Relevant Equations
- KE=1/2mv^2
I think on top of the wedge the KE of both the wedge and block will be same but this fact doesn't take me anywhere. The base length of the wedge is not given. Maybe that would have helped.