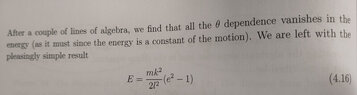Tong Dynamics: cannot cancel angle from orbit energy expression calculation

[jds17]

Hi, I love the lectures by David Tong. Usually I can follow his calculations (but I am not yet so far into the lectures...). But one that I just cannot do is the derivation of the energy in (4.16), the expression being $E = \frac {mk^2} {2 l^2} (e^2 - 1)$, where l is the constant angular momentum of the orbit of the single point particle, m its mass, V(r) = - k/r the expression for the potential and e the eccentricity of the orbit.
I just don't see how using the expression $\frac {dr} {d\theta} = \frac {r_0 e \sin(\theta)} {(1+e \cos(\theta))^2}$ (page 59) in the expression of the energy using the effective potential cancels out the angle $\theta$. Of course it has to work since the energy is a constant of motion, but no matter what trigonometric manipulations I use, it does not cancel out the angle.
In case it is not so readable I have attached the relevant sections from the lecture

 

[Baluncore]

Are you cancelling units or dimensions?
An angle is a ratio, it has no dimension.

 

[jds17]

Thanks! I know, the angle is dimensionless, but still the energy cannot depend on the angle.

I just found why I could not continue with the calculation: I left the radius r in the expression for the energy, but I need to expand it in terms of r_0, theta and the eccentricity as well! It is getting late here. I will do the calculation tomorrow.