Torque and Force Equilibrium in a Rotating Plank

[Izekid]

I have soluted these so but I need an explanation of what I've done.
An even 2,23m long plank is turn-able around its one end. The plank is hold up in an horisontial way with a vertical upp-force on 268 N The force works at 1,52 from the turn-able point. Decide the planks mass.

What I did was I took 268(The force)*1,52(to the turning spot)/2,23(the plank lenght)=182,67

Then I took 268*0,71(the rest of the plank)=190,28

Then I added these too together 182,67+190,28=372,4=37,4kg

Why did I do this? Ppl who didn't understand my English please look at the pic I drow.

The Second problem I didn't understand how I solved either It just popped up the solution

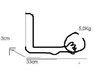
The problem was: Ulla holds a 5kg heavy thing in her hand , with her underarm horisontial. The bicepsmuscle is fastened in the underarm with 3cm from the elbow. The thing is 33cm from the bicepsmuscle.

a) Decide the up-force on the elbowbone from the bicepsmuscle
b)Decide the down-force on the overarmbone by the elbow. Don't take with the weight of the arm

a) I took 5(the weight)*9,82(the acceleration)*33(the distance) / 3(The other distance) = 540N that's ok I understand that

b)Took 540-49,8(5*9,82)=490 why did I do that? don't understand why but it was right... please explain

Regarding Ize

 

[Päällikkö]

Please, please do explain. I've got no idea why you've done what you've done, and the attachments are not working (yet, as they haven't been approved).

The moment of force must equal 0 to keep the Planck from rotating.
\mathbf{M} = \mathbf{r} \times \mathbf{F} = \mathbf{0}
Can you find the two forces and their distances from the point of rotation?
Remember that the force mg can be drawn from the center of mass.

 

[Izekid]

:(

As this is hard swedish words it is really hard to translate, maybe you know Swedish(though you are from Finland) then I maybe can write this in swedish, or maybe that isn't allowed. Can't translate any better sorry... so I hope the Pictures will be allowed soon

 

[Päällikkö]

Is the Planck supposed to be "fatter", as in the picture (I can see them now)? If so, I don't think the mass can be determined, as we won't be able to find the center of mass.

I did understand what you meant in the problem, it's your calculations that are confusing, as you don't explain them anywhere. Although the answer in #1 is close to the correct one, I'm unsure about your method.

 

[Izekid]

nope... its just because the text didnt fit into the plank ... so it even all over the place... well tell me how to do then... don't care about my calculations

 

[Päällikkö]

|\mathbf{M}| = |\mathbf{r} \times \mathbf{F}|
= |\mathbf{r}||\mathbf{F}|\sin\theta = 0
As \theta is 90^o (for both forces), \sin 90^o = 1, we can write the equation: M = Fr.
There is a force (F) applied 1,52 m from the non-moving end. This force (magnitude 268 N) generates a torque of: 268 N * 1,52 m = 407,36 Nm.

The Planck's weight causes a torque to the opposite direction. The center of mass is located at the center of the (supposedly homogenous) Planck, so r for the plack's weight is 2,23 m / 2 = 1,115 m. Now, can you determine how much the Planck must weigh in order to cancel F's effect?