mancity
- 26
- 2
- Homework Statement
- A delivery truck is carrying a 120-kg refrigerator. The refrigerator is 2.20 m tall and 85.0 cm wide. The refrigerator is facing sideways and is prevented from sliding. What is the maximum acceleration that the truck can have before the refrigerator begins to tip over? Assume that the center of gravity of the refrigerator is located at its geometrical center.
- Relevant Equations
- Torque=Fr
The solution lists out mg(b/2)=ma(h/2) and then proceeds to solve for a.
I am a bit stuck on how the initial equation is listed - why is the (b/2) swapped with the (h/2)? (namely, why isn't the equation mg(h/2)=ma(b/2)? My logic for this is y-direction and x-direction )
I feel that I am missing a fundamental concept here
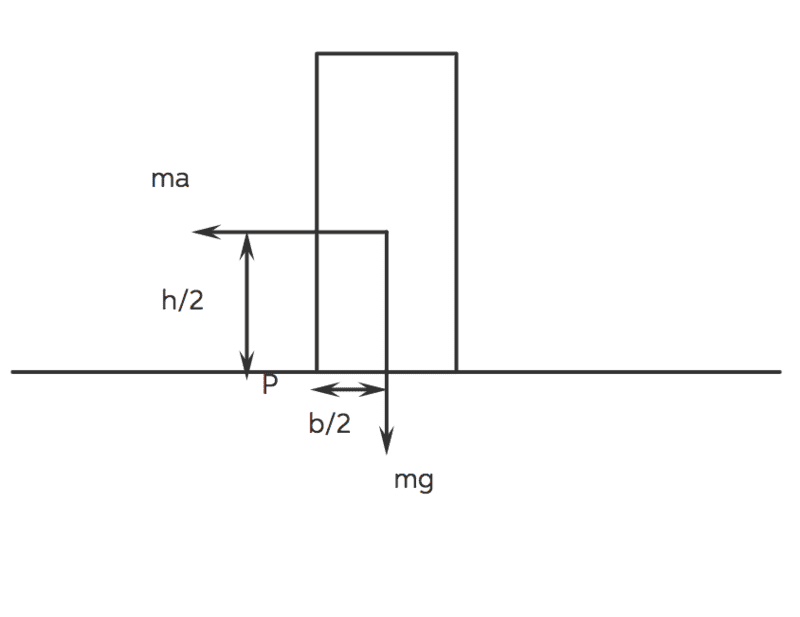
I am a bit stuck on how the initial equation is listed - why is the (b/2) swapped with the (h/2)? (namely, why isn't the equation mg(h/2)=ma(b/2)? My logic for this is y-direction and x-direction )
I feel that I am missing a fundamental concept here