Torque on a Pivot Point With Multiple Forces and Different Directions

[rosedog09]

Homework Statement

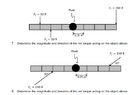
(Questions 7 and 8) Determine the magnitude and net torque acting on the object shown above. (See attached screenshot with figures)

Relevant Equations

T = F*r*sin(angle)

F = force
R= radius
Angle = angle of force

My AP Physics notes state that counterclockwise is generally positive and clockwise is generally negative. This makes sense to me and means forces on opposite sides of the pivot point which act in opposite directions will work together, and this is the logic I applied to answer the problems.

Instead of following this rule, my teacher is saying I should use the direction of the force (i.e two forces acting on opposite sides and in opposite directions of the pivot point will work against each other), but this does not make sense to me as applying and upward force to one side and a downward force to the other will result in a larger net rotation. Could someone explain this to me? Thanks in advance.

P.S Dont take online AP Physics :(

My Work

7.
Net Torque = -100(1) + 50(.5) - 50(.75) = -112.5 Nm

8. Net Torque = -100(.75)(sin30) - 150(.5)(sin30) = -75 Nm

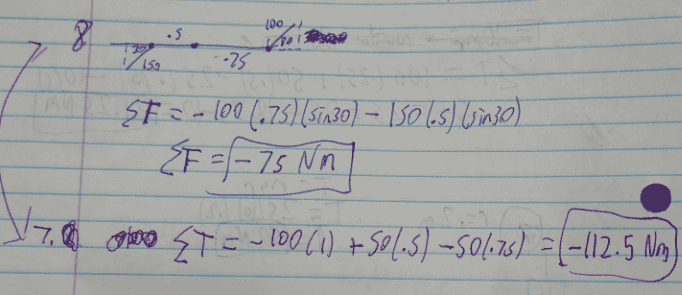
Teacher Comments

I understand I should probably just trust my teacher, but the online program I am enrolled in has had multiple faulty answer keys and teacher misunderstandings to date, and I would like a more thorough explanation of my error.

 

[haruspex]

7.
Net Torque = -100(1) + 50(.5) - 50(.75) = -112.5 Nm

Is the 50N at -.75m acting clockwise or anticlockwise?

8. Net Torque = -100(.75)(sin30) - 150(.5)(sin30) = -75 Nm

Yes.

 

[rosedog09]

7. Ok, I see my mistake, that would make the equation
-100(1)-50(.5)+50(.75) = - 87.5

8. If that is correct, what principle or equation could I show to prove my work to my teacher?

 

[haruspex]

7. Ok, I see my mistake, that would make the equation
-100(1)-50(.5)+50(.75) = - 87.5

8. If that is correct, what principle or equation could I show to prove my work to my teacher?

The second sentence is wrong. It should read
"F3 is down, so it is negative, and it acts to the right of the pivot, so that is positive, which makes the torque negative."

 

[rosedog09]

The second sentence is wrong. It should read
"F3 is down, so it is negative, and it acts to the right of the pivot, so that is positive, which makes the torque negative."

Isn't force 3 to the left of the pivot point?

My bigger issue is I don't understand why I am not getting credit for question 8.

 

[Lnewqban]

Isn't force 3 to the left of the pivot point?

My bigger issue is I don't understand why I am not getting credit for question 8.

The result is matematically correct as it is the addition of two negative values.
However, we are not sure about the exact statement of your teacher.

Perhaps the location of the signs in the equation?
For the moment induced by F1, the negative sign should be associated to the vertical component of the force (-50 N).
For the moment induced by F2, the negative sign should be associated to the distance (-0.5 m).

 

[haruspex]

Isn't force 3 to the left of the pivot point?

Sorry, got confused by the two questions being in the wrong order in the "teacher comments ". Let me try again…
Using exactly the same argument in 8 as is used in 7:
F1 is down, so it is negative, and it acts to the right of the pivot, so that is positive, which makes the torque negative;
F2 is up, so it is positive, and it acts to the left of the pivot, so that is negative, which makes the torque negative.