dcmf
- 16
- 5
- Homework Statement
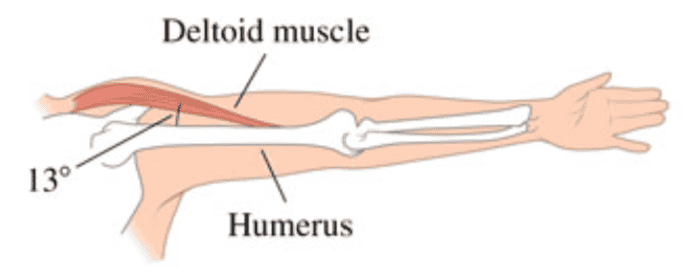
- A woman lifts a 3.6-kg barbell in each hand with her arm in a horizontal position at the side of her body and holds it there for 3 s (see the figure below). What force does the deltoid muscle in her shoulder exert on the humerus bone while holding the barbell? The deltoid attaches 13 cm from the shoulder joint and makes a 13 degree angle with the humerus. The barbell in her hand is 0.55 m from the shoulder joint, and the center of mass of her 4.0-kg arm is 0.24 m from the joint.
- Relevant Equations
- Tnet, T=Flsinθ, Fg=mg
Here's a picture the question provided.
I tried solving this question two ways (assuming the axis of rotation is at the shoulder joint) and am getting wildly different answers.
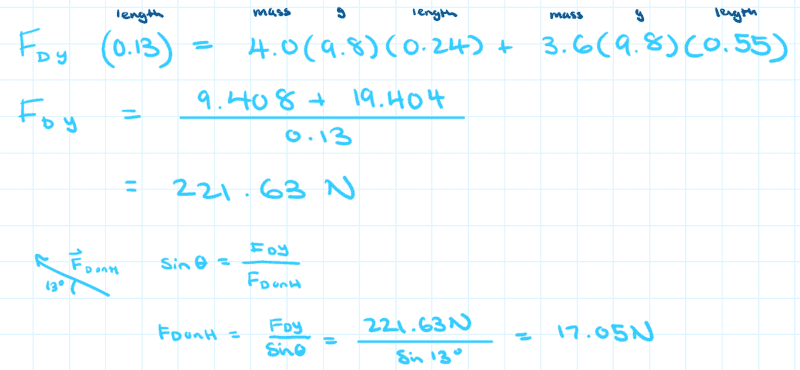
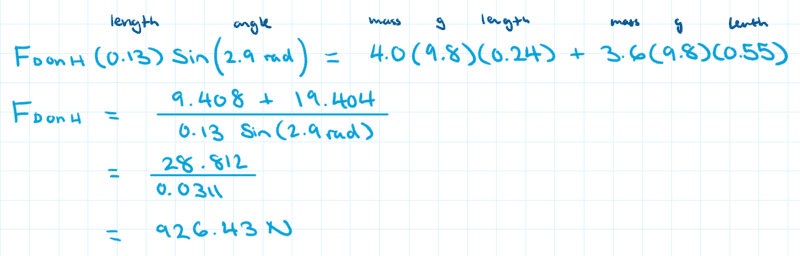
Some potential reasons there's a discrepancy:
- I'm not super confident about my use of the torque equation (T=FlSinθ), especially the angle part, which I think needs radians as an input
- Question mentioned something about 3 seconds but I never used that in any of my calculations and this is a one-part question so its not as if it could be used later on
Thanks in advance!
I tried solving this question two ways (assuming the axis of rotation is at the shoulder joint) and am getting wildly different answers.
Some potential reasons there's a discrepancy:
- I'm not super confident about my use of the torque equation (T=FlSinθ), especially the angle part, which I think needs radians as an input
- Question mentioned something about 3 seconds but I never used that in any of my calculations and this is a one-part question so its not as if it could be used later on
Thanks in advance!