- #1
_Bd_
- 109
- 0
Hi, I am working on a project that needs some rotation around a central axis. I was looking over at some Servos but I don't know how to calculate the torque required by the servo.
I was thinking of doing a simple free body diagram, but as I was drawing it I realized the forces are on the Z axis (assuming an X-Y plane), and therefore do not create a moment around the center axis of the servo, only moments I can think of are parallel to the shaft of the servo.
Heres a very crude image of what I'm trying to do.
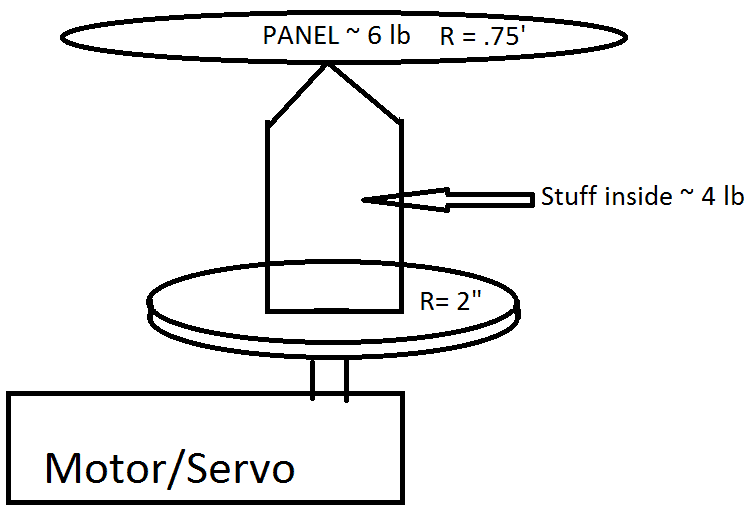
as mentioned, I tried to do a FBD but I couldn't really figure anything out of it. I am thinking it has to do only with the weight applied over the shaft and therefore it doesn't matter how close/far its from the central axis? just the amount pressing would generate more friction or something along those lines, but I'm kind of confused about this.I was thinking of using only T=Ia, (I for disk = 1/2 mr^2) and using m = m_disk + m_beam + m_bigdisk
but still, I don't knwo what alpha is (angular acceleration), I mean, I could probably use any servo's listed Torque and just get alpha from there, but that would be making the assumption that any servo, regardless of its torque output would be able to rotate that? (the idea doesn't make sense)
- Thank you for your help.
I was thinking of doing a simple free body diagram, but as I was drawing it I realized the forces are on the Z axis (assuming an X-Y plane), and therefore do not create a moment around the center axis of the servo, only moments I can think of are parallel to the shaft of the servo.
Heres a very crude image of what I'm trying to do.
as mentioned, I tried to do a FBD but I couldn't really figure anything out of it. I am thinking it has to do only with the weight applied over the shaft and therefore it doesn't matter how close/far its from the central axis? just the amount pressing would generate more friction or something along those lines, but I'm kind of confused about this.I was thinking of using only T=Ia, (I for disk = 1/2 mr^2) and using m = m_disk + m_beam + m_bigdisk
but still, I don't knwo what alpha is (angular acceleration), I mean, I could probably use any servo's listed Torque and just get alpha from there, but that would be making the assumption that any servo, regardless of its torque output would be able to rotate that? (the idea doesn't make sense)
- Thank you for your help.
Last edited: