Torque with Symbolic Notation Problem

[esinn08]

Hi Everyone,

My question is as follows:

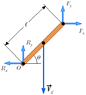
Write the necessary equation of the object shown in Figure P8.4. Take the origin of the torque equation about an axis perpendicular to the page through the point O. (Let clockwise torque be positive and let forces to the right and up be positive. Use q for and Rx, Ry, Fx, Fy, Fg, l, and g as appropriate in your equations.) Find the sum of the forces in the x direction, the y direction, and the total torque. (I hope the picture I attached shows up!)

I've never been good with symbolic notation! I know Rx and Ry will go to zero, since there is no torque through the point of origin. Do I have to break Fg into its x and y components? Any suggestions would be greatly appreciated! Thanks so much!

 

[Nate810]

The equation for the torque about point O is: T = Fx * l - Fg * l * sin(q).The equation for the sum of the forces in the x direction is: Fx = Fg * cos(q).The equation for the sum of the forces in the y direction is: Fy = Fg * sin(q) + Ry - g.The total torque is: T = Fg * l * sin(q).

 

[kyle8921]

I would first like to commend you for seeking help and clarification on this problem. It is important to always fully understand the equations and symbols being used in any scientific context.

To answer your question, yes, you will need to break down Fg into its x and y components. This is because torque is a vector quantity, meaning it has both magnitude and direction. In order to properly calculate the total torque, you will need to take into account the direction of the force.

To calculate the sum of forces in the x and y directions, you can use the equations Fx = Rx + Fgcos(q) and Fy = Ry + Fgsin(q), respectively. This takes into account the vertical and horizontal components of Fg.

As for the total torque, you can use the equation T = Fgl, where l is the distance from the point of origin to the point where the force is applied. This will give you the magnitude of the torque, but remember to take into account the direction as well.

I hope this helps and good luck with your problem! Remember, it's always important to break down complex problems into smaller, more manageable parts.