- #1
Dell
- 590
- 0
the beam below is subjected to a single torque of Mt=10KNm at its centre, G=80GPa
find the distribution of the torque between the 2 components of the central cross section
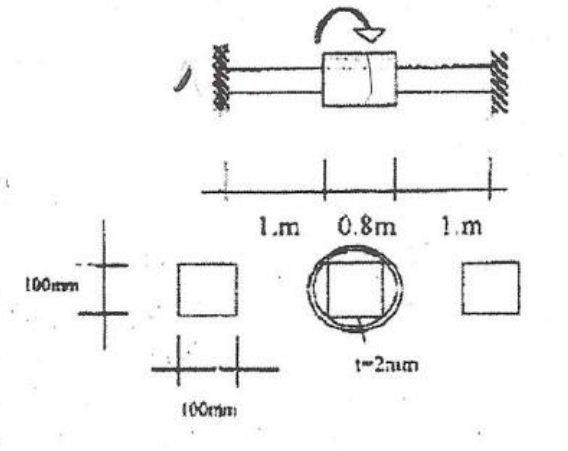
what i have done in similar questions (where i have had one free end) i have chosen T1 and T2 - the relative torque in each of the components and solved using dϕ/dx,- using the fact that the angle of twist from x=1m to x=0.8m must be the same for both components i could solve for T1 and T2 because in all the cases i have solved i knoew that T1+T2=Mt,
in this question i am not sure this is the case since Mt is not the internal Torque in this cross section,
find the distribution of the torque between the 2 components of the central cross section
what i have done in similar questions (where i have had one free end) i have chosen T1 and T2 - the relative torque in each of the components and solved using dϕ/dx,- using the fact that the angle of twist from x=1m to x=0.8m must be the same for both components i could solve for T1 and T2 because in all the cases i have solved i knoew that T1+T2=Mt,
in this question i am not sure this is the case since Mt is not the internal Torque in this cross section,