- #1
Dr Edward
- 9
- 0
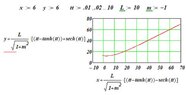
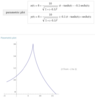
The cusp of the tractrix is on the y-axis.
I have been studying Sreenavisan et al (Mechanism and Machine Theory 45 (2010) 454–466)
Email me for copy, if needed.
What I need is the equation of a tractrix with the hitch point not on the x-axis but on a line below (y=-mx).
Any help would be gratefully received.
Dr Edward
I have been studying Sreenavisan et al (Mechanism and Machine Theory 45 (2010) 454–466)
Email me for copy, if needed.
What I need is the equation of a tractrix with the hitch point not on the x-axis but on a line below (y=-mx).
Any help would be gratefully received.
Dr Edward