Trajectory of an electron traveling near a current-carrying wire

[alesdiazdeo]

Homework Statement

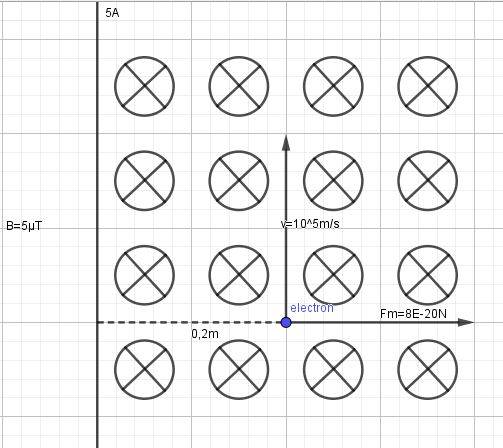
There's an infinite vertical wire which produces 5Amps. An electron is 0.2 meters apart with a velocity of 10^5 m/s in the same direction of the wire. The wire is creating a magnetic field which alters the trajectory of the electron. I need to know to the function which represents it.

Relevant Equations

Fm(magnetic force)=q(v x B) (charge times vectorial multiplication of velocity and magnetic field)
Without vectors it's just Fm=qvB
B(magnetic field)=nu/2pi * I/R (I=current intensity, R=distance)
nu/2pi=2*10^-7 (it's a constant)

B equals 50*10^-7 T (at first instance)
Fm equals 8*10^-20 N (at first instance)

I know Fm is perpendicular to the velocity, and I know the estimation of the trajectory (somewhat similar to the curve y=lnx).

Since I think vertical velocity will be constant, only changing the x component, I tried summing the Fm and the B formula, creating a bigger formula which I think represents the growth on the Y axis of the final desired formula dependent to R. That's what I want, not a formula that depends on time but a formula that depends of the distance to the wire (R).

 

[willem2]

That's what I want, not a formula that depends on time but a formula that depends of the distance to the wire (R).

What is the quantity your formula should compute?

I would describe the trajectory of the electron with an x and y coordinate, where:
x is the distance to the wire
y = the distance the electron has traveled since the start of the experiment. obviously (y = vt)

x will depend on t, an easy computation with Newton's second law (F = ma)
Using y = vt, you can also make x dependent on y.

 

[alesdiazdeo]

There are no preferences, just calculation of the trajectory is my task.

Alright, so I inserted the B formula into the Fm formula and got Fm=1.6*10^-20/R.
Divided it by the mass of the electron and got the acceleration.
Did the integral of that and got v=1,76*10^10*ln|R|+C (which I assume is 0 since R=inf -> v=0)
I thought that was a good representation of the Y axis and the X axis could be represented by 10^5 (constant) but my friend tells me that v (on the X axis) also changes with time.

So I'm lost again.

 

[BvU]

Since I think vertical velocity will be constant

What makes you think that ?

$\$

 

[alesdiazdeo]

What makes you think that ?

$\$

That the initial statement was that; but of course v is only constant in module, not as a vector, as it varies with F=qvB.