- #36
- 8,032
- 869
Where does the refrence input (x_ref) come from? Is this what measures surface irregularities?
deamonata said:I will try this in a MATLAB simulation tomorrow and get back to you but it looks sensible, one question though? what is V_offset?
deamonata said:Ok so update. I have now got the system successfully modeled. and the response matches the physical devicemThe model is shown below:
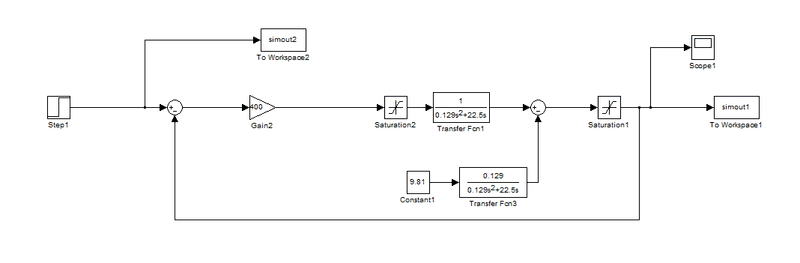
.