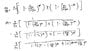- #1
fonseh
- 529
- 2
Homework Statement
I need help when changing the formula of the yellow circled part to red-circled part ...
Homework Equations
The Attempt at a Solution
I tried , but i didnt get what the author got ... Here's my working ... Which part of my working is wrong ?