Transformation of Tensor Components

[FluidStu]

In the transformation of tensor components when changing the co-ordinate system, can someone explain the following:

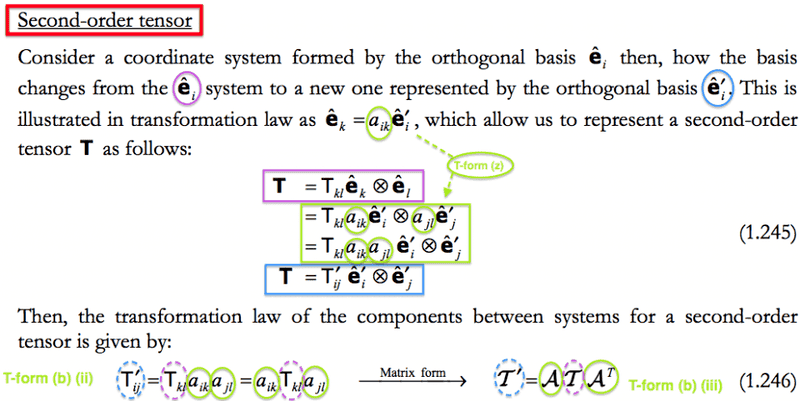
Firstly, what is the point in re-writing the indicial form (on the left) as a_ikT_kla_jl? Since we're representing the components in a matrix, and the transformation matrix is also a matrix, aren't we violating the non-commutativity of matrix multiplication (AB ≠ BA)?

Secondly, how does this mean A T A^T in matrix form? Why are we transposing the matrix?

Thanks in advance

 

[ShayanJ]

Firstly, what is the point in re-writing the indicial form (on the left) as aikTklajl? Since we're representing the components in a matrix, and the transformation matrix is also a matrix, aren't we violating the non-commutativity of matrix multiplication (AB ≠ BA)?

$\mathcal A$,etc. refers to the matrices themselves but $a_{ik}$,etc. refers to the elements of those matrices. So the $a_{ik}$s are just numbers and commute with each other.
Actually there is no need to rearrange them in that way but the author seems to think that it makes things more clear.

Secondly, how does this mean $\mathbf{A T A^{T}}$ in matrix form? Why are we transposing the matrix?

Remember the rule for matrix multiplication? It reads like $(AB)_{ij}=\sum_k A_{ik} B_{kj}$, which, if we accept the rule that repeated indices are summed over, becomes $(AB)_{ij}=A_{ik} B_{kj}$.
So its clear that $a_{ik}T_{kl}$ is actually $C=\mathcal{AT}$. Now we have $c_{il} a_{jl}$. Now if I define $d_{lj}=a_{jl}$, the result becomes $c_{il} d_{lj}$ which is clearly the product of two matrices. The first is $\mathcal{AT}$ and the second was defined as a matrix that has its rows and columns swapped(because I swapped l and j in $a_{jl}$ to get $d_{lj}$). So its clear that the second matrix is $\mathcal{A}^T$ and so the whole product is $\mathcal{ATA}^T$.

 

[FluidStu]

$\mathcal A$,etc. refers to the matrices themselves but $a_{ik}$,etc. refers to the elements of those matrices. So the $a_{ik}$s are just numbers and commute with each other.
Actually there is no need to rearrange them in that way but the author seems to think that it makes things more clear.

Remember the rule for matrix multiplication? It reads like $(AB)_{ij}=\sum_k A_{ik} B_{kj}$, which, if we accept the rule that repeated indices are summed over, becomes $(AB)_{ij}=A_{ik} B_{kj}$.
So its clear that $a_{ik}T_{kl}$ is actually $C=\mathcal{AT}$. Now we have $c_{il} a_{jl}$. Now if I define $d_{lj}=a_{jl}$, the result becomes $c_{il} d_{lj}$ which is clearly the product of two matrices. The first is $\mathcal{AT}$ and the second was defined as a matrix that has its rows and columns swapped(because I swapped l and j in $a_{jl}$ to get $d_{lj}$). So its clear that the second matrix is $\mathcal{A}^T$ and so the whole product is $\mathcal{ATA}^T$.

Got it! Thanks :)