Vanilla Gorilla
- 78
- 24
- TL;DR Summary
- Is it correct to say that a bunch of tensor products of all the basis vectors and covectors composing a general tensor M, multiplied by the components of M, lead to the transformation rule for M?
So, I've been watching eigenchris's video series "Tensors for Beginners" on YouTube. I am currently on video 14. I am a complete beginner and just want some clarification on if I'm truly understanding the material.
Basically, is everything below this correct?
In summary of the derivation of the transformation rules for a general tensor $$M$$, using algebraic notation, we just write the product of the components of the tensor $$M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$, with its basis vectors and basis covectors, where $$\vec {e}_{subscript}$$ represents basis vectors, and $$\epsilon^{superscript}$$ represents basis covectors.
This looks like $$\large {M = M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h} \otimes_{n=1}^h {\vec {e}_{n_1}} \otimes_{p=1}^g {\epsilon^{p_1}}}$$
Where $$\large {\otimes_{n=1}^h {\vec {e}_{n_1}} \otimes_{p=1}^g {\epsilon^{p_1}}}$$ is basically just representative of a bunch of tensor products of all the basis vectors and covectors which compose $$M$$ in reference to the definition of tensors as

(Note that I use the notation $$\otimes_{n=1}^h$$ to denote a series of tensor products from $$n=1$$ to $$h$$)
Then, we use the covector and vector rules given here,
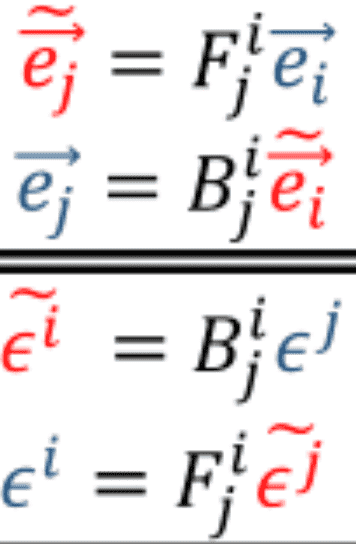
Substitute those into the formula given previously,
$$\large {M = M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h} \otimes_{n=1}^h {\vec {e}_{n_1}} \otimes_{p=1}^g {\epsilon^{p_1}}}$$
Use linearity to bring the forward and/or backward transforms next to $$M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$, with the backward transforms in front of $$M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$, and the forward transforms behind it. I note this detail because I'm 99% sure we don't have commutativity with tensors in general; please correct me if I'm wrong about that, though!
All these transforms in conjunction act on $$M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$ to give $$\tilde {M}_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$
The same general process can be done in reverse to convert $$\tilde {M}_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$ to give $$M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$
P.S., I'm not always great at articulating my thoughts, so my apologies if this question isn't clear.
Basically, is everything below this correct?
In summary of the derivation of the transformation rules for a general tensor $$M$$, using algebraic notation, we just write the product of the components of the tensor $$M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$, with its basis vectors and basis covectors, where $$\vec {e}_{subscript}$$ represents basis vectors, and $$\epsilon^{superscript}$$ represents basis covectors.
This looks like $$\large {M = M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h} \otimes_{n=1}^h {\vec {e}_{n_1}} \otimes_{p=1}^g {\epsilon^{p_1}}}$$
Where $$\large {\otimes_{n=1}^h {\vec {e}_{n_1}} \otimes_{p=1}^g {\epsilon^{p_1}}}$$ is basically just representative of a bunch of tensor products of all the basis vectors and covectors which compose $$M$$ in reference to the definition of tensors as
(Note that I use the notation $$\otimes_{n=1}^h$$ to denote a series of tensor products from $$n=1$$ to $$h$$)
Then, we use the covector and vector rules given here,
Substitute those into the formula given previously,
$$\large {M = M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h} \otimes_{n=1}^h {\vec {e}_{n_1}} \otimes_{p=1}^g {\epsilon^{p_1}}}$$
Use linearity to bring the forward and/or backward transforms next to $$M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$, with the backward transforms in front of $$M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$, and the forward transforms behind it. I note this detail because I'm 99% sure we don't have commutativity with tensors in general; please correct me if I'm wrong about that, though!
All these transforms in conjunction act on $$M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$ to give $$\tilde {M}_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$
The same general process can be done in reverse to convert $$\tilde {M}_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$ to give $$M_{c_1, ~ c_2, ~ c_3,... ~ c_g}^{v_1, ~ v_2, ~ v_3,... ~ v_h}$$
P.S., I'm not always great at articulating my thoughts, so my apologies if this question isn't clear.