Transformations for isotropy in terms of math

[gionole]

Probably, my last question about isotropy. This is the last thing that I want to double check.

We know that mathematically, passive and active transformation are both the same. In passive, coordinate frame is moved and nothing else, while in active frame, objects are moved and coordinate frame stays the same.

I'm trying to show that I can get the same mathematics by using active and passive for isotropy detection.

Experiment we can do consists of the system that includes earth and ball where ball is dropping to earth from some height.

In passive, we get the following math:

$\ddot y = -\frac{d}{dy}(gy)$
$\ddot y' = -\frac{d}{dy}(gycos\theta)$ (in rotated frame)

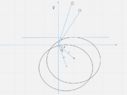
In active(look at the attached image), I rotate earth and ball counter-clockwise by some $\theta$ angle. Note that calculations of old and new coordinate of the points(after rotation and before rotation) are given by the same mathematics as in passive, so I'm on the right track. $y' = -xsin\theta + ycos\theta$ and $x' = xcos\theta + ysin\theta$(there's no prime concept here as we only got one fixed frame, but I call the new coordinates after rotation to be primed)

Now, what I do is: in 1st experiment, we got the same thing $\ddot y = -\frac{d}{dy}(gy)$. In 2nd experiment, after earth and ball rotated, I write the following thing: $\ddot y = -\frac{d}{dy}g(xsin\theta - ycos\theta)$ (I replace $y$ by $xsin\theta - ycos\theta$). The reason why I replace by such thing is that after we did rotating of earth, it got moved as well, so potential energy can't be represented by $mgy$ anymore. So I find by how much earth got moved in $y$ direction, which is given by $-xsin\theta + ycos\theta - (-y) = -xsin\theta + ycos\theta +y$ and then any point where the ball is can be given by $y - (-xsin\theta + ycos\theta +y) = xsin\theta - ycos\theta$ and then plugging in $\ddot y = -\frac{d}{dy}(gy)$. Also note that on the left side, I don't replace it, because it would be incorrect, as we're still trying to find acceleration in the same $y$ frame.

So I end up with $\ddot y = -\frac{d}{dy}g(xsin\theta - ycos\theta)$ which results in $\ddot y = \frac{d}{dy}(gycos\theta)$ . Problem is this result doesn't have "-" in front of it, while from passive transformation calculations, it does. where did I make a mistake and how do I end up with the exact same math ?

 

[renormalize]

Problem is this result doesn't have "-" in front of it, while from passive transformation calculations, it does. where did I make a mistake and how do I end up with the exact same math ?

Consider a 2D object in relation to a set of 2D cartesian axes. If you rotate the object (active transformation), say counterclockwise, it's equivalent to rotating the axes (passive transformation) clockwise. In other words:
Active rotation by angle $\theta$ $\Longleftrightarrow$ Passive rotation by angle $-\theta$.
So you need to flip the sign of the rotation-angle between your two calculations.