- #1
muna580
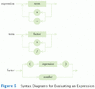
I am creating a class that will transform a basic arithmetic expression from infix to postfix (Reverse Polish Notation (RPN)). Then after then, it will evaluate the postfix expression and give the answer.
I have having a little trouble with the operators (+,-,/,0*, and %). Like, I have to create a method called hasHigherPrecedence(char c1, char c2), which returns a boolean saying where c1 has a higher precedence than c2. But I don't really know hwo to create this method. Can someone help me.
I have having a little trouble with the operators (+,-,/,0*, and %). Like, I have to create a method called hasHigherPrecedence(char c1, char c2), which returns a boolean saying where c1 has a higher precedence than c2. But I don't really know hwo to create this method. Can someone help me.