Transmission Line Model (TLM) End Resistance (Re)

[Azaxa]

Hi guys.

I'm looking into the modelling of a transmission line model (TLM) and feel that I'm understanding it fairly well. Although, one parameter keeps popping up with very little explanation as to what it actually is.

It seems that to characterize contact resistance for a e.g. GaAs TLM with AuGe ohmic contacts, that the contact resistance cannot just be characterized by the sheet resistance beneath the contact (Rsk) and the semiconductor resistance (Rsh) when these two are not equal. Many resources direct me towards Re in this case.

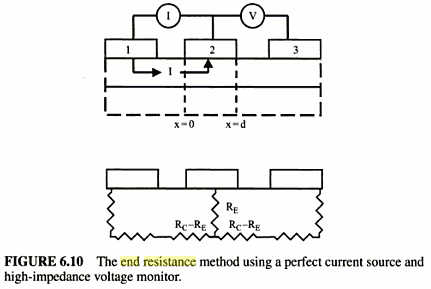
Now, the measurement of Re appears simple, with current flowing between two contacts the voltage is measured from the end contact and a neighbouring unloaded contact, contacts 2 and 3, and this value is divided by the current between contacts 1 and 2 (fig. 6.10).

)

It can be characterized as:

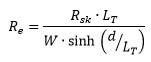
where
Rsk = Sheet resistance beneath ohmic contact,
W = width of the contact,
d = length of the contact,
Lt = transfer length (the length from the front of the contact to where the current is 1/e*io beneath the contact).

My question is:
-Is Re the resistance from Lt to the end of the contact?
-Is Re the resistance blocking current from dispersing from the contact to the next (unloaded) contact?

P.S. the reason I believe this is because if this is the case then and increase in Lt would reduce the area from Lt to end of the contact (x=d) whereas the beginning of the contact (x=0) will have a larger area, contributing to a decrease in contact resistance (Rc) but the "leftover" current after x=Lt will be more dense due to the decrease in area at the contact end. Of course, with greater with this will reduce the resistance of both Rc and Re and finally 1/sinh(d/Lt) or sech(d/Lt) shows that there's an exponential decrease in resistance due to the ratio that current density is shared (Rc/Re = cosh(d/Lt)).
I hope this helps with explanations.

Thanks, in advance.

 

[mark726]

Hi there,

Thank you for your question about contact resistance in transmission line models. You are correct in your understanding that Re is the resistance from the transfer length (Lt) to the end of the contact. This is also known as the "end resistance" and it represents the resistance that current encounters as it flows from the contact to the next (unloaded) contact.

The transfer length (Lt) is an important parameter in characterizing contact resistance because it represents the length at which the current begins to spread out from the contact. As you mentioned, an increase in Lt would result in a decrease in contact resistance due to a decrease in the area from Lt to the end of the contact. This is because the current is able to spread out more, reducing the density and therefore the resistance.

Additionally, the ratio of current density between the contact resistance (Rc) and the end resistance (Re) is also important in determining the overall contact resistance. As you pointed out, the ratio can be described by 1/sinh(d/Lt) or sech(d/Lt), which shows an exponential decrease in resistance as the ratio increases. This highlights the importance of optimizing both the contact resistance and the end resistance in order to minimize overall contact resistance in a TLM.

I hope this helps to clarify the role of Re in characterizing contact resistance in TLMs. If you have any further questions, please don't hesitate to ask.