Transmission of torque using friction

[Juanda]

TL;DR Summary

I want to derive the formula for the transmission of torque through friction.

I am trying to obtain the expression for the potential transmission of torque using friction.

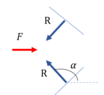
I could derive the formula assuming constant pressure between planar surfaces.

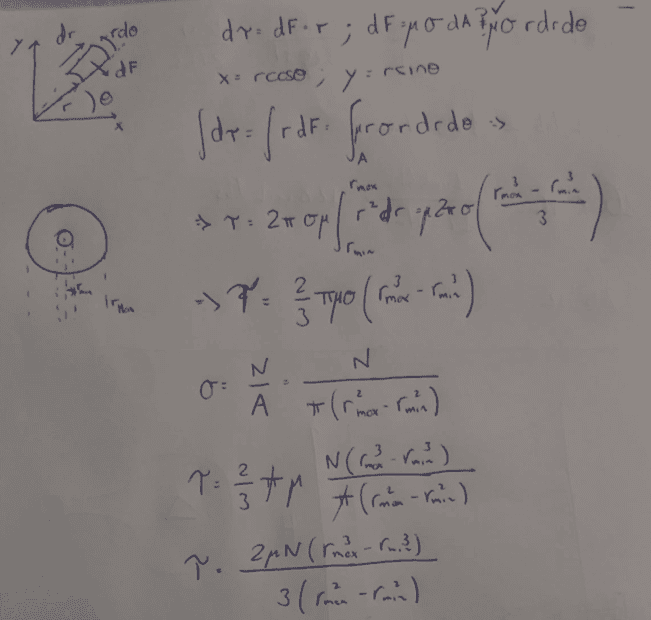
To have it in LATEX so it is easier to read, this is the expression for the torque transmission using friction.
$$\tau=\frac{2\mu N(r_M^3-r_m^3)}{3(r_M^2-r_m^2)}$$

This is the same as what I later found in this video of Youtube so I'm fairly confident that the result is correct.
(Note: He is using $F$ instead of $N$ for the normal force and also his disks are solid without a hole in the middle)

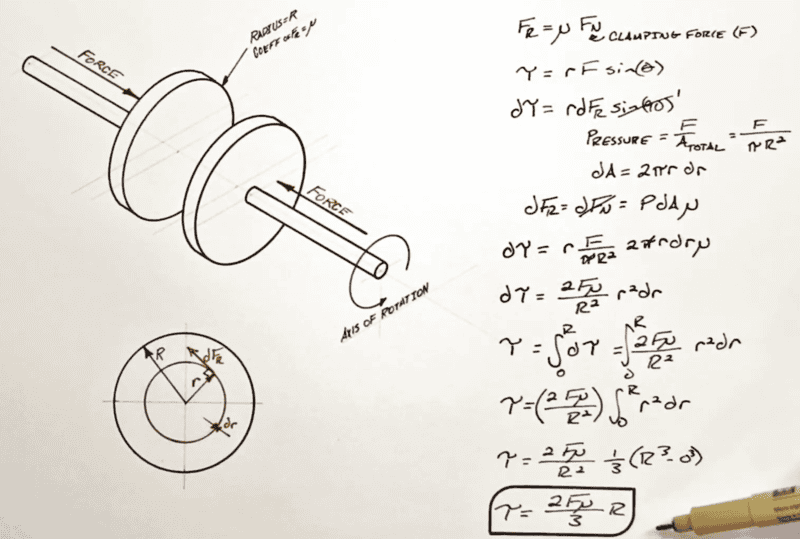
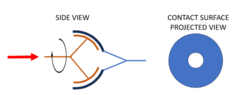
I'm now interested in knowing a similar but a little bit more complex case. Spherical contact instead of planar contact. Not necessarily half a sphere but that would be the case with the biggest contact patch.

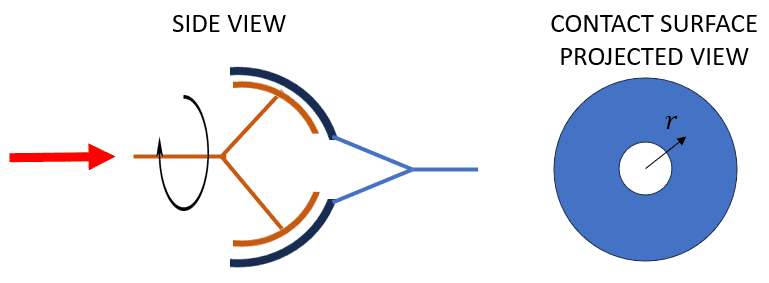
In this scenario, assuming a constant pressure makes less sense. As the contact patch becomes more tangential to the force, I assume the normal force between surfaces will decrease. How would you obtain the normal pressure between surfaces as a function of the angular position under study? Because of the rotational symmetry, I believe it'd be possible to express that function as $\theta (r)$ (see the diagram of the projected area) but I don't know how. Once that normal pressure is known, I hope to be able to derive the torque in a similar way as I did for the planar case.

 

[Juanda]

In this scenario, assuming a constant pressure makes less sense. As the contact patch becomes more tangential to the force, I assume the normal force between surfaces will decrease.

By the way, is it possible to derive from this statement (if true) that a planar case with the same projected radius will always have greater friction than a spherical one?
The leverage would be greater in that case since more force would be acting near the edge of the disc.

 

[Baluncore]

With the spherical case, I assume the shafts remain coaxial, or you will have a friction drive with a Cos(theta) speed reduction ratio.

There are two ways of applying force to the spherical contact surface.

1. As a spherical radial force, the outer sphere is shrunk onto the inner, or the inner expanded against the outer. That is a different problem, related to the elasticity of the material.

2. As an axial force. Reduce the problem to axial and radial components. Think of the contact surfaces as having small dx and dr orthogonal steps. Since the force is axial, the pressure is axial. The radial component of force does not exist, so radial pressure need not be considered. The radius of the sphere then becomes equivalent to the radius of the flat disc, with the same torque equation.

If the spheres were elastically deformed by the force, the problem would become more complex, and begin to approach case 1, or a drum brake.

 

[Juanda]

With the spherical case, I assume the shafts remain coaxial, or you will have a friction drive with a Cos(theta) speed reduction ratio.

It'd be mostly coaxial. Maybe a small misalignment of ~5º or so but that's it.

2. As an axial force. Reduce the problem to axial and radial components. Think of the contact surfaces as having small dx and dr orthogonal steps. Since the force is axial, the pressure is axial. The radial component of force does not exist, so radial pressure need not be considered. The radius of the sphere then becomes equivalent to the radius of the flat disc, with the same torque equation.

If the spheres were elastically deformed by the force, the problem would become more complex, and begin to approach case 1, or a drum brake.

It is closer to the second scenario you described. But I'm still having trouble obtaining the pressure distribution. I'll try to draw a few diagrams to better explain where I'm getting lost.

For the flat contact, I believe it's clear but I'll add this diagram because it's a good foundation for the spherical case.

Assuming a constant pressure distribution I can then do the integral shown in #1 to find the torque.

For the spherical case though I can't obtain the function $\sigma (r)$.

I know that the integral of the horizontal component of $\sigma$ must be the axial force but that's it. I don't know the function itself. And even if I had it I believe I cannot integrate in the projected surface to follow a procedure similar to the one used for the flat surfaces because near the shaft there'll be a greater concentration of surface.

These complications are why I wanted to confirm if the flat case can be considered a conservative scenario. I believe it'd produce greater friction as mentioned in post #2.

 

[A.T.]

Since the force is axial, the pressure is axial. The radial component of force does not exist, so radial pressure need not be considered.

Just because the total force is only axial, doesn't mean there are no radial forces, which cancel each other, but still affect the pressure distribution.

 

[Juanda]

Just because the total force is only axial, doesn't mean there are no radial forces, which cancel each other, but still affect the pressure distribution.

Agreed. That's what I meant with this:

For the spherical case though I can't obtain the function $\sigma (r)$.
View attachment 337999
I know that the integral of the horizontal component of $\sigma$ must be the axial force but that's it. I don't know the function itself.

The normal pressure will be greater in that case which will contribute to a greater friction but the leverage will be smaller than in the flat case because I'm expecting the normal pressure to be more focussed near the shaft.
If calculating the spherical case turns out to be too difficult I was hoping there's at least a way to "prove" that the combinations of the 2 effects (greater pressure + smaller leverage) turn out in an overall smaller rotational friction when compared with the flat case which is already calculated and can work as a safety margin.

 

[Baluncore]

Just because the total force is only axial, doesn't mean there are no radial forces, which cancel each other, but still affect the pressure distribution.

I think the effect of the changed pressure distribution, is cancelled by the increased surface area of the sphere, compared to the disc.

Without elastic deformation, or wear, I cannot see how the friction or torque can be different between the disc and the sphere. I believe that force is important, that pressure is a distraction, and you are chasing your tail.

 

[A.T.]

If calculating the spherical case turns out to be too difficult I was hoping there's at least a way to "prove" that the combinations of the 2 effects (greater pressure + smaller leverage) turn out in an overall smaller rotational friction when compared with the flat case which is already calculated and can work as a safety margin.

With respect to the pressure distribution, even the flat case is statically indeterminate, so you have to assume uniform pressure. In the spherical case that assumption is not reasonable anymore, so I don't think you can calculate it without additional assumptions and considering deformation. If it is for safety I would assume the worst case, and add some margin on that.

 

[Juanda]

With respect to the pressure distribution, even the flat case is statically indeterminate, so you have to assume uniform pressure. In the spherical case that assumption is not reasonable anymore, so I don't think you can calculate it without additional assumptions and considering deformation. If it is for safety I would assume the worst case, and add some margin on that.

Yes. My problem at the moment is that, so far, I can't manage to calculate the spherical case which is what I would need to be able to compare both of them.

 

[Lnewqban]

Yes. My problem at the moment is that, so far, I can't manage to calculate the spherical case which is what I would need to be able to compare both of them.

Could you try calculating several conical sections approaching the spherical shape instead?

It seems to me that as the sectional cones tend to the shape of a cylinder, a wedge self-clocking self-locking effect should appear, making the disengage process and a smooth engaging difficult.

 

[256bits]

Yes. My problem at the moment is that, so far, I can't manage to calculate the spherical case which is what I would need to be able to compare both of them.

What is so difficult about it?
Any shaft, solid or hollow, in pure compression has axial stress induced within evenly distributed ( as in the picture in post 4 for the flat contact )
No matter which way one makes a cut through the shaft to make a FBD, the axial forces remain directed along the axis. To have the forces balance out, one would show the stress normal to the cut, and the shear stress perpendicular to the cut. These have to add up to the axial stress.

A spherical cut, symmetrical about the axis of the shaft, would be used to analyze the mating of two spherically matched surfaces. The normal stress would be some angle function, sin, cos, tan ( which you will have to determine ) along the surface. This normal stress is what you are calling the pressure of the mating surfaces.

If one attempts to rotate one mating surfaces against the other, you have a varying N along the surface, a supposed friction factor mu to apply to N. Using some other calculation, one can find the friction of the mating surfaces.

 

[Baluncore]

It seems to me that as the sectional cones tend to the shape of a cylinder, a wedge self-clocking effect should appear, making the disengage process and a smooth engaging difficult.

Self-clocking, or self-locking?
Self-locking requires that one cone is able to move axially. That is not the case with an in-elastic sphere, since the almost-flat front-face prevents further movement once it contacts. That is why the analysis of the inelastic sphere, with only axial force, collapses to that of the disc.

 

[Juanda]

Could you try calculating several conical sections approaching the spherical shape instead?

It seems to me that as the sectional cones tend to the shape of a cylinder, a wedge self-clocking effect should appear, making the disengage process and a smooth engaging difficult.

View attachment 338025

I didn't think about discretizing the problem like that. It could be a valid approach if I can't find the actual pressure distribution on the spherical case.
I'd first need to derive the friction on a conical section with an arbitrary angle. I'll give it a shot and return to confirm if the results are correct.
Also, I guess I should try to keep the "exit" angle of the sphere somewhere around 45º or below so the deformation doesn't cause them to become stuck/wedge with one another because it's something I'd need to avoid for the mechanism I have in mind. Thanks for pointing it out.

 

[Juanda]

What is so difficult about it?
Any shaft, solid or hollow, in pure compression has axial stress induced within evenly distributed ( as in the picture in post 4 for the flat contact )
No matter which way one makes a cut through the shaft to make a FBD, the axial forces remain directed along the axis. To have the forces balance out, one would show the stress normal to the cut, and the shear stress perpendicular to the cut. These have to add up to the axial stress.

A spherical cut, symmetrical about the axis of the shaft, would be used to analyze the mating of two spherically matched surfaces. The normal stress would be some angle function, sin, cos, tan ( which you will have to determine ) along the surface. This normal stress is what you are calling the pressure of the mating surfaces.

If one attempts to rotate one mating surfaces against the other, you have a varying N along the surface, a supposed friction factor mu to apply to N. Using some other calculation, one can find the friction of the mating surfaces.

I marked in bold letters what I find difficult about it. I'm aware of what you describe, but all my attempts to obtain such a function have been unsuccessful so far. It may be trivial to you but I'm definitely having trouble with it.

 

[Lnewqban]

Self-clocking, or self-locking?
Self-locking requires that one cone is able to move axially. That is not the case with an in-elastic sphere, since the almost-flat front-face prevents further movement once it contacts. That is why the analysis of the inelastic sphere, with only axial force, collapses to that of the disc.

Please, excuse the typo.
I meant self-locking, being self-holding perhaps a better term, as happens to Morse tapers used in industrial drill bits, which rely on a heavy rate of radial load over axial load to transmit high torques.

 

[Baluncore]

Also, I guess I should try to keep the "exit" angle of the sphere somewhere around 45º or below so the deformation doesn't cause them to become stuck/wedge with one another because it's something I'd need to avoid for the mechanism I have in mind. Thanks for pointing it out.

Self-locking of a conical surface starts when; Tan(wedge angle) < friction coefficient.
But it requires axial movement of the cone, which, in this case, is prevented by the steeper angle of the front-face.

 

[Lnewqban]

That is not the case with an in-elastic sphere, since the almost-flat front-face prevents further movement once it contacts. That is why the analysis of the inelastic sphere, with only axial force, collapses to that of the disc.

If I understand you correctly, the more "perpendicular" surfaces respect to the shafts prevent any useful frictional effect from the more "perpendicular" surfaces of both spheres (assuming both shapes to be a geometrically perfect match, which is very difficult to achieve in practical fabrication).

Perhaps that is the reason for this shape of clutch not to be usual.
Also, I believe that it can't work as a solution to cases of misalignment between both shafts, because it would induce endless slipping and heat generation, once the clutch tries to "grab".

 

[Juanda]

Self-locking of a conical surface starts when; Tan(wedge angle) < friction coefficient.

I didn't know that relation but it looks familiar. Tan of the angle shows up often in problems related to friction.

But it requires axial movement of the cone, which, in this case, is prevented by the steeper angle of the front-face.

Hhhmmm. I think I see what you're saying. The "male" sphere cannot penetrate further into the female and deform it because the nearly flat top of the sphere makes it impossible. This doesn't happen with cones and that's why they wedge.
Maybe I'm not so restricted regarding the exit angle of the sphere because of that.

 

[Juanda]

If I understand you correctly, the more "perpendicular" surfaces respect to the shafts prevent any useful frictional effect from the more "perpendicular" surfaces of both spheres (assuming both shapes to be a geometrically perfect match, which is very difficult to achieve in practical fabrication).

Perhaps that is the reason for this shape of clutch not to be usual.
Also, I believe that it can't work as a solution to cases of misalignment between both shafts, because it would induce endless slipping and heat generation, once the clutch tries to "grab".

Would you then say that the transmission of torque in the spherical contact case is poorer? Because that's actually what I'm looking for. I would even most likely apply lubrication on it.

 

[Baluncore]

Also, I believe that it can't work as a solution to cases of misalignment between both shafts, because it would induce endless slipping and heat generation, once the clutch tries to "grab".

Think of the construction of a Constant Velocity Joint, that has balls in channels to couple the shafts. The balls move to lie on a half-angle plane, where the differential velocity of the spherical surfaces is zero.

 

[Baluncore]

I would even most likely apply lubrication on it.

I would consider applying a "traction fluid", to transfer torque without material contact.
https://www.santolubes.com/products/santotrac/
http://orbitaltraction.com/technology/elastohydrodynamic-traction-fluid/

 

[Juanda]

I would consider applying a "traction fluid", to transfer torque without material contact.
https://www.santolubes.com/products/santotrac/
http://orbitaltraction.com/technology/elastohydrodynamic-traction-fluid/

I wish I could. I'm thinking of a space application so there are a lot of restrictions around lubricants.
My first thought is to use MoS2 coating or similar.

 

[Baluncore]

In space, continuous sliding friction will need to radiate heat.
Maybe consider a matched permanent-magnet pole-pattern. That will limit torque, without contact, generating less heat when it slips.

 

[Juanda]

In space, continuous sliding friction will need to radiate heat.
Maybe consider a matched permanent-magnet pole-pattern. That will limit torque, without contact, generating less heat when it slips.

In this case, I'll just need to get a 90º turn to activate a mechanism and that's all the action it'll see. Kind of like turning a key.
I'm here trying to find the sort of torque I'd need to turn that key to see if the idea I have in mind is even feasible because I consider the spherical contact important for this application and I couldn't find the answer by myself yet.
If the flat contact surface turns out to be a conservative case (which I think it is) then the idea might have some potential before some other big problem arises on the horizon.

 

[Lnewqban]

Would you then say that the transmission of torque in the spherical contact case is poorer? Because that's actually what I'm looking for. I would even most likely apply lubrication on it.

That would be a combination of universal joint and slipping clutch, working on the kinetic friction zone.

https://en.wikipedia.org/wiki/Constant-velocity_joint

https://en.wikipedia.org/wiki/Clutch

https://en.wikipedia.org/wiki/Torque_converter

The problem I see is that, once both shafts get out of perfect alignment, there will be relative sliding of the male and female surfaces for each turn of the clutch.

That slipping will continuously happen while the device is trying to transfer torque in an efficient way, meaning minimum useful mechanical energy becoming useless and damaging heat.

As traditionally accomplished in cars, gradual transmission of torque (clutch) and its re-direction (joints), have been achieved with separate devices in all industrial applications that I have worked with.

 

[Juanda]

That would be a combination of universal joint and slipping clutch, working on the kinetic friction zone.

https://en.wikipedia.org/wiki/Constant-velocity_joint

https://en.wikipedia.org/wiki/Clutch

https://en.wikipedia.org/wiki/Torque_converter

The problem I see is that, once both shafts get out of perfect alignment, there will be relative sliding of the male and female surfaces for each turn of the clutch.

That slipping will continuously happen while the device is trying to transfer torque in an efficient way, meaning minimum useful mechanical energy becoming useless and damaging heat.

As traditionally accomplished in cars, gradual transmission of torque (clutch) and its re-direction (joints), have been achieved with separate devices in all industrial applications that I have worked with.

Although the equations are similar to that of a clutch, the mechanism I have in mind is not really like that. I'm not worried about continuous operation.
See posts #22 and #24 for more details.
I wish I could share more information more freely but I feel like I'm already cutting it close to the limit.
Still, I'll carefully read the 3 links you shared in case I find some inspiration in them.

 

[Lnewqban]

See posts #22 and #24 for more details.

Sorry, I have missed those while I was working on my last post.
I am sure that you will find a solution for that mechanism, as heat is not a problem.

 

[Juanda]

I didn't think about discretizing the problem like that. It could be a valid approach if I can't find the actual pressure distribution on the spherical case.
I'd first need to derive the friction on a conical section with an arbitrary angle. I'll give it a shot and return to confirm if the results are correct.

@Lnewqban This is my approach to the conical section. It's more of a combination of intuition and a leap of faith so let's see if it makes sense.

I first simplified the conical section to two flat angled surfaces.

Because it's static we can say:
$$\sum F_x = 0 \rightarrow F+2R\cos (\alpha)=0 \rightarrow R=\frac{-F}{2\cos(\alpha)}$$
We can see from that how the angle causes the reaction to be bigger in magnitude just as expected.

If we assume a constant pressure field, which I consider reasonable in this scenario, then $R$ can be expressed as:
$$R=\sigma A$$
From the 2 previous equations, it is possible to obtain the magnitude of the pressure field:
$$\sigma A = \frac{-F}{2\cos(\alpha)} \rightarrow \sigma = \frac{-F}{2A\cos(\alpha)}$$

Here now comes the leap of faith. I couldn't apply Calculus the right way to obtain the expression for a continuous conical section but, based on the previous result, I feel the answer must be like this.

$$\sigma = \left | \frac{-F}{A\cos(\alpha)} \right |\left \{ \alpha = \theta+\pi/2; \cos(\theta+\pi/2)=-\sin(\theta) \right \}\rightarrow \sigma = \frac{F}{A\sin(\theta)}$$

The 3 things to know about the last equation are:

1. I got rid of the $-$ because it's related to whether it's going left or right and I don't care about that.
2. The $2$ disappears because it's not 2 separated sections as it was before.
3. I hope I didn't mistake the trigonometric identity to use the angle of the cone $\theta$.

The area $A$ of the conical section can be calculated and I think I have that under control. Just in case I'll post a picture but I don't think it's necessary to focus on that.

Note: I used $\beta$ for the conical angle because I used $\theta$ for the variable. This may cause some confusion because I also used $\theta$ before in the drawing made in PPT to describe the angle of the cone...If all that's correct, the next step would be to check the transmission of torque due to that pressure field, distance to the center, and friction coefficient.
Then, the last bit would be to discretize the sphere in a significant number of those cones.

What do you think?

 

[Lnewqban]

Please, see:
https://en.wikipedia.org/wiki/Wedge

 

[Juanda]

Please, see:
https://en.wikipedia.org/wiki/Wedge

The reasoning in the article makes sense but I don't see why I'm getting a different result... Both things definitely cannot be simultaneously true and I can't find the error.

When I used Newton in post #28, the $\cos\alpha$ showed up.

I first simplified the conical section to two flat angled surfaces.
View attachment 338068

Because it's static we can say:
$$\sum F_x = 0 \rightarrow F+2R\cos (\alpha)=0 \rightarrow R=\frac{-F}{2\cos(\alpha)}$$
We can see from that how the angle causes the reaction to be bigger in magnitude just as expected.

But in the Wiki article, they use a conservation of energy argument, and then it's dependent on the tangent instead of the cosine.

Could both be true but be referring to different things or did I make a mistake?

 

[erobz]

@Lnewqban This is my approach to the conical section. It's more of a combination of intuition and a leap of faith so let's see if it makes sense.

I first simplified the conical section to two flat angled surfaces.
View attachment 338068

Because it's static we can say:
$$\sum F_x = 0 \rightarrow F+2R\cos (\alpha)=0 \rightarrow R=\frac{-F}{2\cos(\alpha)}$$
We can see from that how the angle causes the reaction to be bigger in magnitude just as expected.

Isn't there a frictional force component of $2 \mu R \cos \theta$ missing from this force balance?

 

[Juanda]

Isn't there a frictional force component of $2 \mu R \cos \theta$ missing from this force balance?

I think you're right. I should have added the frictional force tangent to the surfaces as well.
In that case, the expression I get is:
$$\sum F_x=0\rightarrow F+2R\cos(\alpha)+2\mu R\cos(\alpha+\frac{\pi}{2})=0\rightarrow F+2R(\cos(\alpha)-\mu\sin(\alpha))=0$$
$$R=\frac{-F}{2(\cos(\alpha)-\mu\sin(\alpha))}$$
Then, the normal stress to the surface would be again:
$$\sigma =\frac{R}{A}$$
If I tried to slide the block in the $z$ direction (in or out of the screen) while applying $F$, then the opposing force would be $\mu R$ I believe.

 

[khamlichi]

Please note that there are two regimes of friction: uniform pressure and uniform wear. At the beginning the pressure is uniform and wear is uneven. But, after the running-in phase, the wear becomes uniform and pressure adjustes unevenly. This is important in practice since there exists noticeable difference between the two situations.