Trapezoid method converges faster than the Simpson method

[Cloruro de potasio]

TL;DR

Is it possible that the trapezoid method converges faster than the simpson method?

Good Morning,

I have been doing computer practices in C ++, and for an integration practice, the trapezoid method converges faster than the Simpson method. The function to be integrated is a first class elliptical integral of the form:

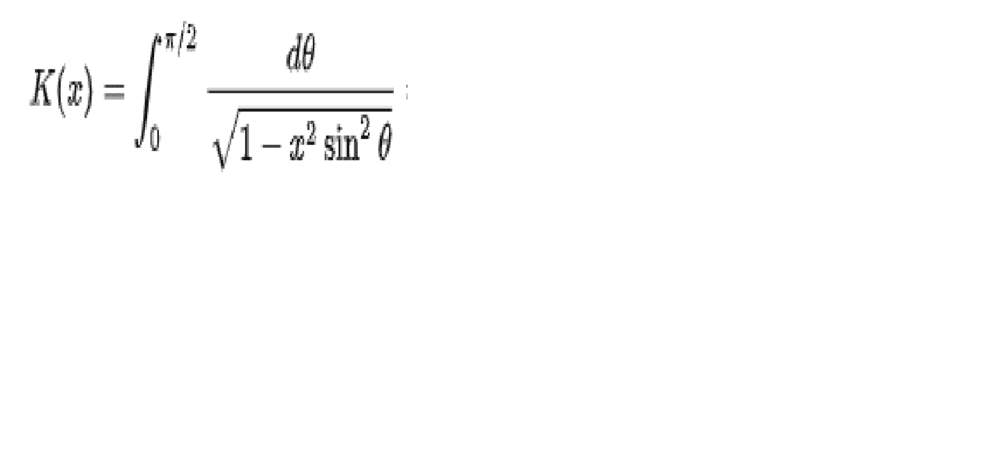
Where k is bounded between [0,1). I have been thinking about the reason for this fact, and one of the hypotheses I have is that both the second derivative (which is used to determine the error level of the trapezoid method), and the fourth (which is used to determine the Simpson method error level), diverge in pi / 2, so it is not possible to calculate the maximum error level.

This is the graph that I get for the decimal logarithm of the error vs the number of intervals used:

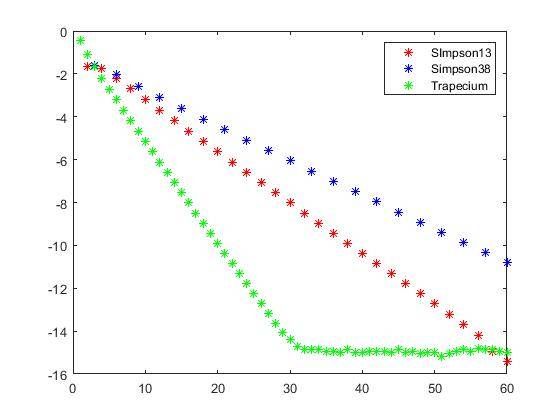
Does anyone know why this happens?

 

[jasonRF]

I believe this has to do with the fact that the trapezoidal rule converges very quickly when integrating a periodic function over an entire period. You are only integrating over half of the period, but your integrand has symmetry so your integral is simply 1/2 of the integral over the full period and you should still get the fast convergence.

The trapezoidal rule really is a go-to technique for smooth, periodic integrands.

 

[Cloruro de potasio]

Okay, thanks, and this phenomenon, why does it happen? I've been searching on several websites but I don't understand very well ...

 

[QuantumQuest]

Summary:: Is it possible that the trapezoid method converges faster than the simpson method?

I have been thinking about the reason for this fact, and one of the hypotheses I have is that both the second derivative (which is used to determine the error level of the trapezoid method), and the fourth (which is used to determine the Simpson method error level), diverge in pi / 2, so it is not possible to calculate the maximum error level.

For the trapezoidal approach, an upper bound for the absolute value of error is

$|E_T| \leq \frac{b - a}{12}h^2 max|f''(x)|$, where the integral is calculated between $a$ and $b$ on the $x$-axis and $h = \Delta x = \frac{b - a}{n}$, $n$ is the number of sub-intervals, $max$ refers to the interval $[a, b]$ and $f''$ is continuous on $[a, b]$.

In practice, we usually cannot find the exact value of $max|f''(x)|$, so we have to estimate a reasonable upper bound or the worst possible value of error instead. So, if $M$ is any upper bound of $max|f''(x)|$ then $|E_T| \leq \frac{b - a}{12}h^2 M$. We find the best possible value for $M$ and then proceed to evaluate $E_T$. In order to decrease $E_T$ for a given $M$ we decrease $h$.

For Simpson Rule, a useful (absolute) value for error is

$|E_S| \leq \frac{b - a}{180} h^4 max |f^{(4)}(x)|$, where $max$ refers to the interval $[a, b]$ and $f^{(4)}$ is continuous on $(a, b)$. As in the trapezoidal approach, we usually cannot find the exact value of $max |f^{(4)}(x)|$ along the integration interval. So, again, we find some reasonable upper bound $M$.

For the first of the above formulas of upper bounds of error, we start from the Mean Value Theorem and extend it, so we get that if $f$ and $f'$ are continuous on $[a,b]$ and $f'$ is differentiable on $(a,b)$, there is a number $c$ on $(a,b)$ such that $\int_{a}^{b} f(x)dx = T - \frac{b - a}{12} h^2 f''(c)$ and for the second, we start from the Generalized Mean Value Theorem. For the proof of both of these you can search on the net.

 

[Cloruro de potasio]

Okay, thanks, I knew these formulas, what happens is that since you have to integrate between 0 and 2π and in 2π the second and fourth derivatives diverge, it is difficult to get the maximum error level ...

And is there any explanation why, in this particular case, the trapezoid method converges faster?