Travel time of a particle suspended from an elastic string

[gnits]

Homework Statement

To find the time of travel of a particle on an elastic string

Relevant Equations

F=ma

Hi,

Can anyone please help me with the following:

I have found the velocity of projection, no problem, it is v = 2*sqrt(10)

Also, in obtaining this value, I have also found the extension in the string when in equilibrium, it is x = 2

Now on to the time of flight.

The given answer is: t = ( PI/(2 * sqrt(40) ) + sqrt(2)/sqrt(10)

So the motion is in two parts, one when the string is stretched and so pulling on the mass, and one where the string is unstretched and so the mass is simply a projectile.

I am going to try to calculate the time taken to rise from 1m below A to A. This is the part of the motion which is that of a projectile. And I believe form the given answer that I zshould expect to obtain sqrt(2)/sqrt(10). I do not.

Hopefully, someone can show me where this method is in error:

Here's a diagram:

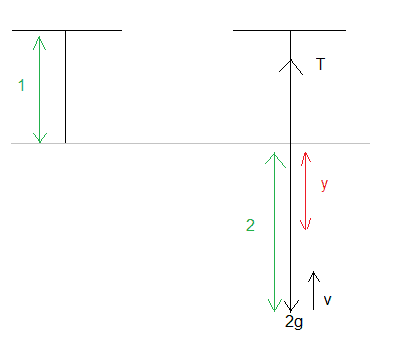
On the left is just the string, on the right is the string stretched by the 2g weight.

Let the general position of the particle be y below the unstretched level. The tension in the string is T. Hookes law gives T = Kx/a where K is the modulus of elasticity (here = 10), a is the natural length (here = 1), and the extention is x (in the diagram this is equal to y).

So we have T = 10y

Now equating forces gives (F = ma):

10y - 2g = 2 * acceleration

And so we have: acceleration = 5y - g = 5y - 10

Now, as accerleration = dv/dt = (ds/dt)(dv/ds)=v (dv/ds) we have:

v dv/dy = 5y - 10 and so separating variables gives:

integral(v dv) = integral(5y-10 dy) and so we have:

(1/2)v^2 = (5/2)y^2 - 10y + c

And using v = 2*sqrt(10) when y = 2 leads to c = 30

and so we have (1/2)v^2 = (5/2)y^2 - 10y + 30 which is

v^2 = 5y^2 - 20y + 60

So we can now put in y = 0 to obtain the speed of the mass at the moment that the string becomes slack. From here I use v = u - gt to obtain t - the time to go from slack to A. This leads to a different answer from the book.

Thanks for any help in pointing out my error,
Mitch.

 

[haruspex]

the velocity of projection, no problem, it is v = 2*sqrt(10)

Not so. The string helps it up.

Edit2: having realized the 2g is a typo for 2kg, I withdraw the above.

Edit: also, I would take the 1m as the relaxed length. If you provide the book answer we can determine which reading is correct.

 

[TSny]

Now, as accerleration = dv/dt = (ds/dt)(dv/ds)=v (dv/ds) we have:

v dv/dy = 5y - 10

Be careful with signs here. In setting up F = ma you chose the upward direction as positive. But y increases as you move downward.

You may write dv/dt = (dv/dy)(dy/dt), as this is just the chain rule. But does dy/dt = v or does dy/dt = -v?

 

[gnits]

Be careful with signs here. In setting up F = ma you chose the upward direction as positive. But y increases as you move downward.

You may write dv/dt = (dv/dy)(dy/dt), as this is just the chain rule. But does dy/dt = v or does dy/dt = -v?

Thank you very much, that was it, the writing of dy/dt as v was the mistake. I should have written it, as you say, as -v. Then I obtain the book answer of sqrt(2)/sqrt(10). Thanks so much for spotting this. I will be more careful in future.

My remaining task is to find the time taken to go from the initial point of projection to the point 1m below A. The form of the answer PI/(2 * sqrt(20)) makes me think that this part of the motion should be treated as Simple Harmonic Motion. Is this in fact the case? If the particle had simply been released then I can see that it would be, but is it still Simple Harmonic Motion if the particle is initially projected with some velocity?

(If I were to try to use my equation of "v as a function of y" to solve for "v as a function of t" I would get: dy/dt=sqrt(20y-5y^2+20) and this leads to (20y - 5^2+10)^(-1/2) dy = dt and integrating the LHS isn't pretty and given that the context of the question is a chapter on SHM I'm thinking that there must be a smarter way)

Thanks for any help.

 

[gnits]

Thank you very much, that was it, the writing of dy/dt as v was the mistake. I should have written it, as you say, as -v. Then I obtain the book answer of sqrt(2)/sqrt(10). Thanks so much for spotting this. I will be more careful in future.

My remaining task is to find the time taken to go from the initial point of projection to the point 1m below A. The form of the answer PI/(2 * sqrt(20)) makes me think that this part of the motion should be treated as Simple Harmonic Motion. Is this in fact the case? If the particle had simply been released then I can see that it would be, but is it still Simple Harmonic Motion if the particle is initially projected with some velocity?

(If I were to try to use my equation of "v as a function of y" to solve for "v as a function of t" I would get: dy/dt=sqrt(20y-5y^2+20) and this leads to (20y - 5^2+10)^(-1/2) dy = dt and integrating the LHS isn't pretty and given that the context of the question is a chapter on SHM I'm thinking that there must be a smarter way)

Thanks for any help.

Ok, I was not too far off, my mistake was thinking that the integral was unpleasant, in fact the integral is simply -(1/sqrt(5))*asin((2-x)/(2*sqrt(2))) and it all works out to the book answer.

Thanks again for all of your help,
Mitch.

 

[sysprog]

I love this. The youngster does and shows his work, is well assisted, and is appreciative. This is a big part of why PF is a great site.

 

[haruspex]

The mass is given as 2g, the relaxed length as 1m and the modulus as 10N. In equilibrium the extension should be 2mm, not 2m.
I presume the 2g was a typo for 2kg.