Traveling wave solution notation

[baseballfan_ny]

TL;DR Summary

Is there a difference between writing $f(-kx + \omega*t)$ and $f(kx - \omega*t)$ for right traveling waves?

This is probably kind of dumb, but it's really bothering me for some reason. I originally saw traveling wave solutions to the wave equation as $f(kx−\omega t)$ for right traveling (as t gets bigger, x needs to be bigger to "match" it's previous value) and $f(kx+\omega t)$ for left-traveling waves. And that all made sense to me. Then I saw some people writing $f(−kx+\omega t)$ for right-travelling waves. I'm pretty sure it's the same thing right? Like this also says that as t gets larger x needs to be larger to match it's original value? Is it just a notation preference when choosing between the two?

My confusion sort of stemmed from seeing the derivation of the reflection and transmittance for a traveling wave at a boundary:

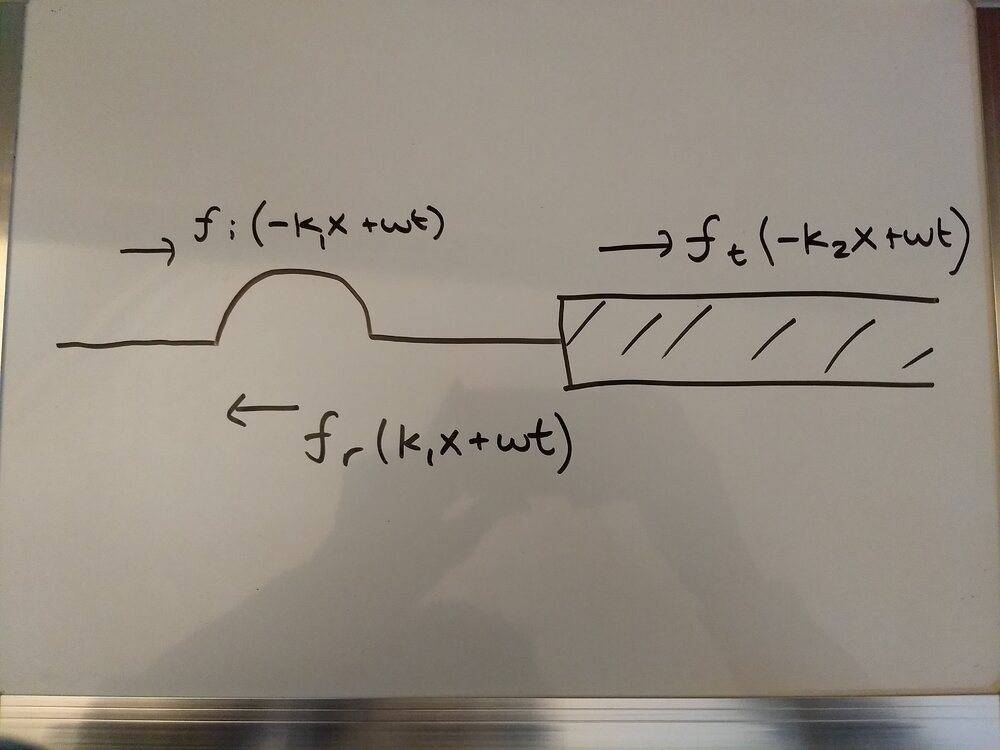
where $f_i$ is the incident pulse, $f_r$ is the reflected, and $f_t$ is the transmitted.

The derivation for the reflectance and transmittance is like:

Because the wave function has to be continuous at the boundary, x = 0:
$f_i(\omega t) + f_r(\omega t) = f_t(\omega t)$

Because it's space derivative has to be continuous at x = 0 so it doesn't have infinite acceleration:
$-k_1 f'_i(\omega t) + k_1 f'_r(\omega t) = -k_2 f'_t(\omega t)$

And then integrating both sides of the second equation with respect to t
$\frac {-k_1} {\omega} f_i(\omega t) + \frac {k_1} {\omega} f_i(\omega t) = \frac {-k_2} {\omega} f_t(\omega t)$

And then by the dispersion relation $\omega = v*k$ so $\frac {k} {\omega} = \frac {1} {v}$ ...
$\frac {-1} {v_1} f_i(\omega t) + \frac {1} {v_1} f_r(\omega t) = \frac {-1} {v_2} f_t(\omega t)$

which gives $-v_2 (f_i(\omega t) - f_r(\omega t)) = -v_1 (f_t(\omega t))$

and then we can solve this equation and the continuity of f and get

$f_r(\omega t) = \frac {v_2 - v_1} {v_1 + v_2} f_i(\omega t) = R f_i(\omega t)$
$f_t(\omega t) = \frac {2v_2} {v_1 + v_2} f_i(\omega t) = T f_i(\omega t)$

The problem is is that if I do this whole thing by saying the incident, right traveling wave is $f_i(k_1x - \omega t)$, the reflected left traveling wave is $f_r(k_1 + \omega t)$, and the transmitted wave is $f_t(k_2x - \omega t)$

I get these two equations to solve (using the same methods as above)

$f_i(\omega t) + f_r(\omega t) = f_t(\omega t)$
$v_2(f_i(\omega t) + f_r(\omega t)) = v_1 f_t(\omega t)$

which gives me $f_r = \frac {v_2 - v_1} {v_1 - v_2} f_i = -f_i$ and $f_t = 0$.

So why is it necessary to write the right traveling waves as $f_i(-kx + \omega t)$ and why does $f_i(kx - \omega t)$ not work instead?

 

[Dale]

Summary:: Is there a difference between writing $f(-kx + \omega*t)$ and $f(kx - \omega*t)$ for right traveling waves?

It depends if $f$ is even or not. If $f$ is even then there is no difference. Otherwise there is a difference.

 

[baseballfan_ny]

It depends if $f$ is even or not. If $f$ is even then there is no difference. Otherwise there is a difference.

Ok. I'm not sure I 100% understand the difference. I drew some odd waves and they still seem to shift right with both forms.

The wave I was dealing with in post 1 is even, so I based on what you wrote I would expect both forms to give the same R and T. Turns out I made a stupid algebra mistake in this line of post 1:

fi(ωt)+fr(ωt)=ft(ωt)

The $f_i$ and $f_t$ should have a negative argument, and then I follow through with the rest of the algebra and get the same answer -- as they're both even.

 

[Dale]

I drew some odd waves and they still seem to shift right with both forms.

Yes, they will still shift right, but they will have a different shape with the two forms.

 

[vela]

Summary:: Is there a difference between writing $f(-kx + \omega*t)$ and $f(kx - \omega*t)$ for right traveling waves?

They both represent a wave traveling to the right. Obviously, for a given wave, you'd use different $f$s in the two cases.