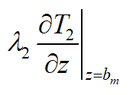Treatment of source term on the boundary: FEA and Comsol

[madani]

TL;DR Summary

Treatment of source term on the boundary: Finite Element Analysis using Comsol Multiphysics

I would like to solve a coupled system of two PDEs using Comsol for the following geometry:

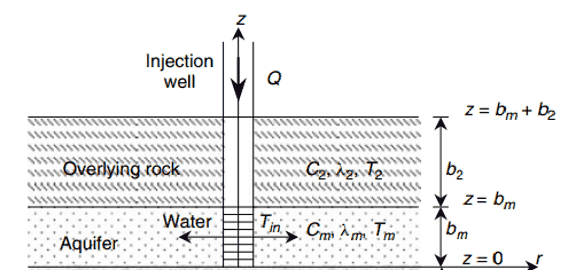
Equation 1 (valid for 0⩽Z⩽bm):

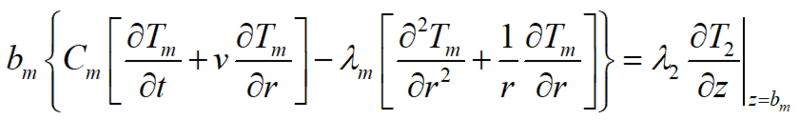
The initial and boundary conditions are:
Tm(r,t→0)=20
Tm(r→rw,t)=70
Tm(r→∞,t)=20

However, for bm⩽Z⩽bm+b2, the equation to solve is:

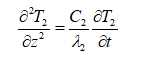
With the following initial and boundary conditions:
T2(r,t→0)=19
T2(z→bm,t)=Tm(r,t)
T2(z→bm+b2,t)=19


Now, to solve the above PDEs, the coefficient form PDE in Comsol can be used. Two adjacent domains can be drawn, with each of which representing each equation mentioned above. However, my question is how to define the source term at the interface between two layers (at z=bm) for the region representing Equation 1. In Comsol, we can add flux/source term to the PDE, which has the following formulation:

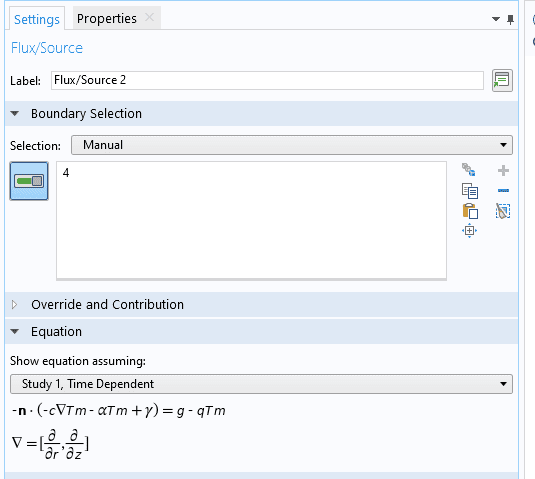
However, the source term $\[{\left. {{\lambda _2}\frac{{\partial {T_2}}}{{\partial z}}} \right|_{z = {b_m}}}\]$ is not in the form provided as in the above picture. I have also tried to add a constraint and add Equation 1 on the interface (z=bm), however, I couldn't see any changes (Please see below pic):

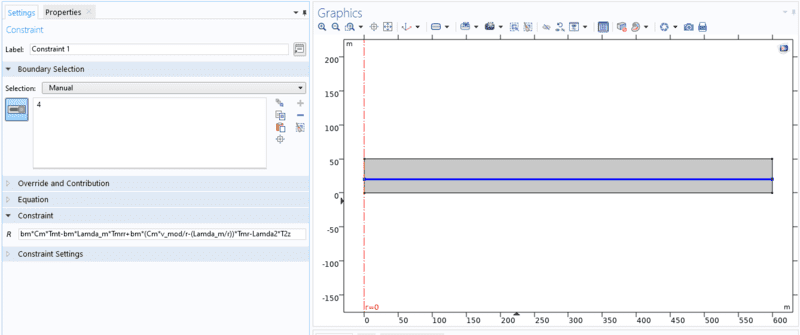
Does anyone know how to add the source term such as this in Comsol?

Thanks in advance!