Jerremy_S
- 8
- 0
Hi All,
Having given a= π/3 Can you explain why b= 5π/3 ?
And Also, where this integral formula comes from? What is it called?
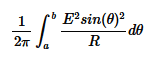
I am going back and forth through my textbooks and I cannot find anything.
A push in the right direction would be appreciated:)
Thanks
Having given a= π/3 Can you explain why b= 5π/3 ?
And Also, where this integral formula comes from? What is it called?
I am going back and forth through my textbooks and I cannot find anything.
A push in the right direction would be appreciated:)
Thanks