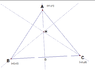
- #1
alijan kk
- 130
- 5
Homework Statement
in the proof of triangle altitudes concurrency , i have found the equation of the Altitude AD,
x(x2-x3)+y(y2-y3)-x1(x2-x3)-y1(y2-y3)
Homework Equations
The Attempt at a Solution
In the book other altitude equations are written by symmetry,
how is the idea of symmetry is used here ? , .
Attachments
Last edited by a moderator: