Triangle Challenge: Prove 2.5<PQ/QR<3

[anemone]

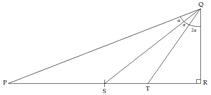
In a triangle $PQR$ right-angled at $R$, the median through $Q$ bisects the angle between $QP$ and the bisector of $\angle Q$.

Prove that $2.5<\dfrac{PQ}{QR}<3$.

 

[MarkFL]

My solution:

Spoiler

Please refer to the following diagram:

View attachment 3974

We see that:

$$\sec^2(4\alpha)=\left(\frac{\overline{PQ}}{\overline{QR}}\right)^2$$

And we also find:

$$4\tan^2(3\alpha)+1=\left(\frac{\overline{PQ}}{\overline{QR}}\right)^2$$

And so this implies:

$$f(\alpha)=4\tan^2(3\alpha)-\sec^2(4\alpha)+1=0$$

Using a numeric root-finding technique, we find the smallest positive root (the only applicable root) is:

$$\alpha\approx0.29630697598921511618$$

And thus:

$$\sec(4\alpha)\approx2.6589670819169940791$$

Hence:

$$2.5<\frac{\overline{PQ}}{\overline{QR}}<3$$

 

[anemone]

Thanks, MarkFL for participating and the really smart and intelligent way to prove this challenge!

I want to share the solution of other too:

Spoiler

If we use MarkFL's provided diagram, the Sine rule tells us, both from triangles $PQS$ and $QSR$ that

$\dfrac{QS}{\sin P}=\dfrac{PS}{\sin \theta}$

$\dfrac{QS}{\sin 90^{\circ}}=\dfrac{RS}{\sin 3\theta}$

Since $PS=RS$, we obtain $\sin 3\theta \sin P=\sin \theta$. However, $P=90^{\circ}-4\theta$, thus we get $\sin 3\theta \cos 4\theta=\sin \theta$.

Note that

$\dfrac{PQ}{QR}=\dfrac{1}{\cos 4\theta}=\dfrac{\sin 3\theta}{\sin \theta}=3-4\sin^2 \theta$

This shows that $\dfrac{PQ}{QR}<3$.

Using $\dfrac{PQ}{QR}=3-4\sin^2 \theta$, it's easy to compute $\cos 2\theta=\dfrac{\dfrac{PQ}{QR}-1}{2}$.

Hence,

$\dfrac{QR}{PQ}=\cos 4\theta=\dfrac{1}{2}\left(\dfrac{PQ}{QR}-1\right)^2-1$

Suppose $\dfrac{PQ}{QR}\le 2.5=\dfrac{5}{2}$. Then $\left(\dfrac{PQ}{QR}-1\right)^2\le \dfrac{9}{4}$ and $\dfrac{QR}{PQ}\ge \dfrac{2}{5}$.

Thus,

$\dfrac{2}{5}\le \dfrac{QR}{PQ}=\dfrac{1}{2}\left(\dfrac{PQ}{QR}-1\right)^2-1\le \dfrac{9}{8}-1=\dfrac{1}{8}$, which is absurd.

We conclude then that $\dfrac{QR}{PQ}>\dfrac{5}{2}$ and the proof is done.