Triangle problem from Feynman's exercises

[czakun]

Homework Statement

Deduce formulas:
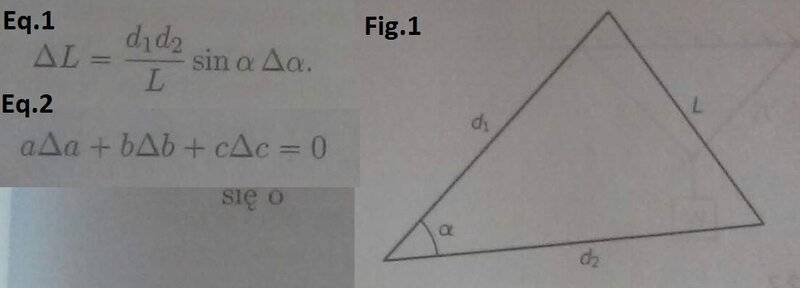
a) how would change side L of triangle, when α angle changes slightly of value Δα for constant remaining sides of triangle i.e. d1 and d2 (fig.1)
b) in rectangular triangle all sides changes their dimensions slightly of values Δa, Δb ,Δc, where c is a hypotenuse. Proove the formula aΔa+bΔb+cΔc=0.

Relevant Equations

aΔa+bΔb+cΔc=0
ΔL=(d1*d2)/L*sinα*Δα

I'm confused about it is not clearly given in task that all the little changes Δ are approaching 0. Especially that Feynman does not mention limits in chapter exercise is for. He is using relatively big values as a little changes (like 4cm). Let's assume that Δ means value is approaching 0.

a) my way to think about this problem is to draw graph L(α) where 0<α<180. We can mark some points on that graph.
for α->0 value of L is equal to absolute value of d1 and d2, L=|d1-d2|,
for α=90, L= sqrt(d1^2+d2^2),
for α->180, L->d1+d2,
but i can't find that mysterious fuction which connects all these points clearly, second is that it gets really complicated. Final answer would be derivative from that mysterouis fuction times dα, dL=L'(α)*dα. It even kinda corresponds to the answer form.
b) isn't that obvious that any constant multiplied by value which reaches 0 is 0?
Is assumption all Δ changes are approaching 0 required for these formulas to be true?
Source: Exercises for the Feynman Lectures, chapter 2, exercise 2.4

 

[mjc123]

a) Are you familiar with the cosine rule?
L² = d₁² + d₂² - 2d₁d₂cosα
b) To say that no change means no change is trivial and pointless. What we are interested in is a small but non-zero change, small enough that, although Δa itself is not negligible, (Δa)² and higher powers may be regarded as negligible. Now, how do you apply Pythagoras to the modified triangle?
(PS Is the formula correct? E.g. if the triangle simply expands by 1%, Δa, Δb and Δc are all positive, so the formula can't be true. Is there some constraint you haven't mentioned?)

 

[erensatik]

a) Are you familiar with the cosine rule?
L² = d₁² + d₂² - 2d₁d₂cosα
b) To say that no change means no change is trivial and pointless. What we are interested in is a small but non-zero change, small enough that, although Δa itself is not negligible, (Δa)² and higher powers may be regarded as negligible. Now, how do you apply Pythagoras to the modified triangle?
(PS Is the formula correct? E.g. if the triangle simply expands by 1%, Δa, Δb and Δc are all positive, so the formula can't be true. Is there some constraint you haven't mentioned?)

Equation in the b part of the question is different in my book. It is a(Δa) + b(Δb) = c(Δc) and it is easy to get with Pythagorean theorem. My question is how it is related with conservation of energy?

 

[Steve4Physics]

Equation in the b part of the question is different in my book. It is a(Δa) + b(Δb) = c(Δc) and it is easy to get with Pythagorean theorem. My question is how it is related with conservation of energy?

Hi @erensatik and welcome to PF.

1) Note that the first 2 posts date back to May 2021! The thread had effectively ended.
2) I guess there is a mistake and the OP meant to ask about aΔa+bΔb-cΔc=0.
3) Why do you think this is related to conservation of energy? Are you thinking about the (Special Relativity) equation $E^2 = (pc)^2 + (m_0c^2)^2$ where the quantities $E$, $pc$ and $mc^2$ are related by the Pythagorean rule?

 

[erensatik]

Hi @erensatik and welcome to PF.

1) Note that the first 2 posts date back to May 2021! The thread had effectively ended.
2) I guess there is a mistake and the OP meant to ask about aΔa+bΔb-cΔc=0.
3) Why do you think this is related to conservation of energy? Are you thinking about the (Special Relativity) equation $E^2 = (pc)^2 + (m_0c^2)^2$ where the quantities $E$, $pc$ and $mc^2$ are related by the Pythagorean rule?

Thanks for the reply. Do you mean to say that I should have posted a new threat? I am new so I don't know much.
The reason I asked this question is the problem OP posted is in chapter 2 of "Exercises for the Feynman Lectures On Physics".Which is a chapter dedicated to energy. I don't know the special relativity equation you posted above.

​

​

 

[Steve4Physics]

Thanks for the reply. Do you mean to say that I should have posted a new threat?

Personally I wouldn't post any threats! But posting a new thread would be appropriate.

the problem OP posted is in chapter 2 of "Exercises for the Feynman Lectures On Physics".Which is a chapter dedicated to energy. I don't know the special relativity equation you posted above.

I don't know why the poblem would be posted in the context of energy. Maybe it's just a maths exercise that has been 'slipped in'. Someone familiar with the Exercises might have more insight.