Remixex
- 57
- 4
- Homework Statement
- Hello everyone, I am having some problems with what the professor calls basic geometry....
Imagine we have our planet Earth divided into two homogeneous segments. Mantle and core. a ray takes off with an angle ##\beta## and travels straight through the mantle a linear distance ##a## which can also be expressed as a surface distance of 110 degrees (to go from degrees to arc distance just multiply by 111.2).
A second ray takes off with angle ##\alpha##, smaller than ##\beta## and enters the core with an incident angle ##\theta_1## and refracts with an outgoing angle ##\theta_2##. Travels through the core, refracts again through the mantle and reaches the surface, creating what's known as a "shadow zone" (P wave shadow zone is between 110 and 140 degrees, but ##\alpha## doesn't necessarily reach exactly at 140 degrees, it's arbitrary)
What are the angles of incidence and refraction? (This will yield the velocity at the core)
- Relevant Equations
- Law of sines, cosines and Snell's law
I have managed to get some of the required distances and angles. I have the distance ##a##, the velocity inside the mantle, the total radius of the Earth ##R_t## as well as mantle and core radii. I have also figured out the angle of incidence, however I cannot get the refracted angle with the available information. I have drawn and created a couple of more distances and angles I have been able to figure out, such as ##\epsilon## which contains the refracted angle, ##\epsilon=\delta+\theta_1## however I do not know how to get ##\delta##...
Any help or direction would be appreciated. I have reached several times at solutions that turn out to be wrong, and I have started over several times. A high resolution version of the image can be found in imgur : (imgur.com)/a/Y0rvkg9
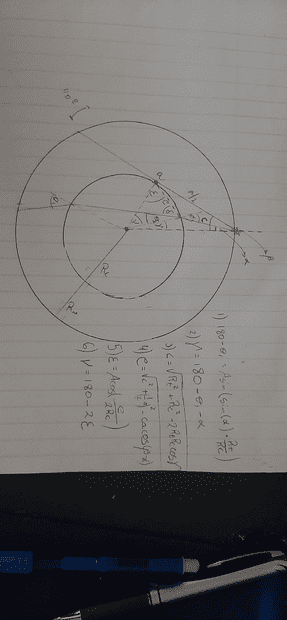
Any help or direction would be appreciated. I have reached several times at solutions that turn out to be wrong, and I have started over several times. A high resolution version of the image can be found in imgur : (imgur.com)/a/Y0rvkg9