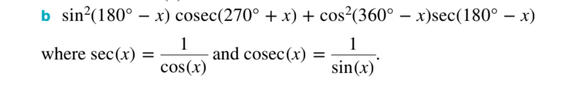Trigonometric Question sin^2(180-x) cosec(270+x) + cos^2(360-x) sec(180-x)

[Yazan975]

View attachment 9012

In this question, I tried this:

sin^2(180-x) cosec(270+x) + cos^2(360-x) sec(180-x), where cosec(x) = 1/sin(x) and sec(x) = 1/cos(x)

-sin^2(180-x) = sin^2(x) and cos^2(x) = cos^2(x)

-The sin^2 and the 1/sin(x) cancle out along with the cos^2 and the 1/cos(x)

Therefore, I am left with sin(x)(270+x) + cos(x)(180-x)

This looks wrong. The answer on the answer sheet is -sec(x). I ask you for help please.

 

[skeeter]

$\csc(270+x) = \dfrac{1}{\sin(270+x)} = \dfrac{1}{\sin(270)\cos{x}+\cos(270)\sin{x}} = \dfrac{1}{-\cos{x}}$

$\sec(180-x) = \dfrac{1}{\cos(180-x)} = \dfrac{1}{\cos(180)\cos{x} + \sin(180)\sin{x}} = \dfrac{1}{-\cos{x}}$

...

$\dfrac{\sin^2{x}}{-\cos{x}} + \dfrac{\cos^2{x}}{-\cos{x}}$

can you finish from here?