Trigonometry - Cricket related word problem

[nmnna]

Homework Statement

A cricket ball is rolled in a straight line down the pitch from immediately alongside one of the stumps at one end of the pitch. Find within what angle its direction of motion lies if it does not miss the wickets at the other end. Take the diameter of the ball as 3 in. and the extreme width of the stumps as 8 in.

Relevant Equations

$$\tan(\alpha) = \frac{opposite \ side}{adjacent \ side}$$

Hello, I don't know anything about cricket, so I'll be grateful if you help me with constructing a diagram for this problem.

Here's my attempt.

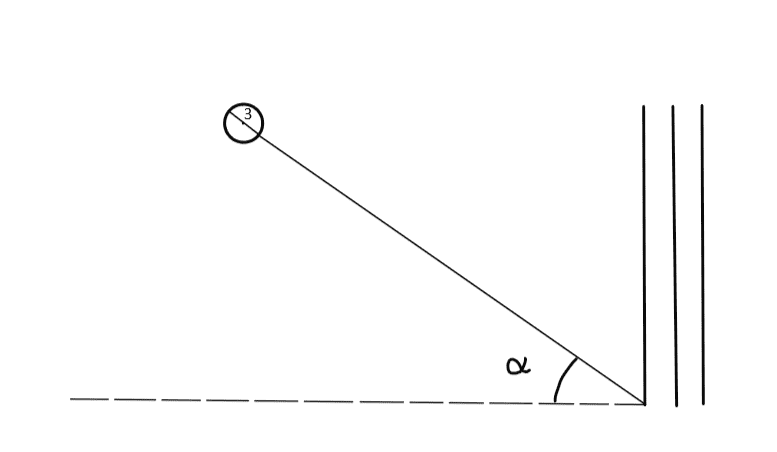
I looked up on the internet and I pretty much get the idea of pitches and wickets, but still cannot connect everything together.
Thank you.

 

[PeroK]

I think what you want is this, where $D$ is the diameter of the ball, $L$ is the length of the pitch (stumps to stumps) and $W$ is the width of the stumps.

 

[nmnna]

I think what you want is this, where $D$ is the diameter of the ball, $L$ is the length of the pitch (stumps to stumps) and $W$ is the width of the stumps.

View attachment 279840

Thank you for your effort.
My understanding.
$$w = 8 in. \ D = 3 in. L = 22 yd = 792 in.$$
The opposite side of alpha $$ = 2(1.5) + 8 = 11 in.$$
So $$\tan(\alpha) = \frac{opposite \ side}{adjacent \ side} = \frac{11}{792} \approx 0.014 \Rightarrow \alpha = \arctan(0.014) \approx 0.802^\circ \approx 48' $$
Is this right?

 

[PeroK]

Looks about right.