- #1
SSG-E
- 60
- 12
- TL;DR Summary
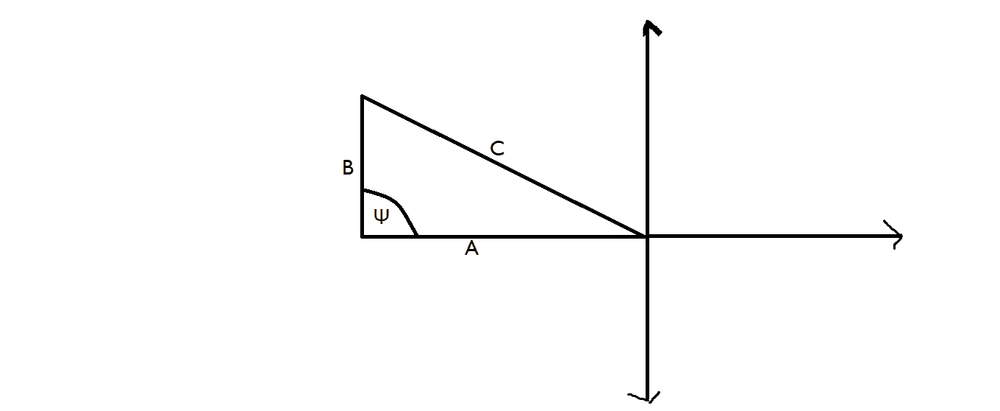
- In case of right angled triangles, C^2 = A^2 +B^2 - 2AB cos(Ψ) is shortened to C^2 = A^2 +B^2 because the cosine of the angle "Ψ" which is 90° is equal to 0. But how is its cosine equal to 0.
I