- #1
Sparkypedia
- 15
- 0
Good Evening all,
Let me start by introducing myself, my name is Alex and I am in the final stages of an Electronic Engineering degree. This is not directly 'homework'. It will take me a little while to set the scene so feel free to get a cup of tea!
One of my modules (Wireless Sensor Networks) has a project that involves using 3 wireless motes and a base station. For those that have not come across this, it is simply 3 wireless sensor platforms that relay their respective data to a hub (base-station) that is connected to a computer serial port. The project was meant to be fairly straightforward; each mote has a series of embedded sensors. I was meant to pick one and then relay each motes data back to the computer and display it in a homemade GUI. I have already accomplished all of this quite successfully. (I chose to use the embedded light dependent resistors (LDR's) as my sensors.
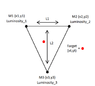
For some brownie points (this is not in the projects spec) I thought it would be interesting if I could track the co-ordinates of a target moving around within the sensor grid. The idea being that I turn all the lights off and then send someone with a torch walking around room. The mote closest to the target would give the highest sensor reading.
The problem with this is I cannot use normal trilateration, as I do not know the distance between each mote and the target. All I have to go on is the motes LDR readings which can vary depending on the light source anywhere between readings of 3 and 1300.
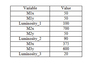
Known Variables
Mote No.1,2,3 X,Y coordinates
Mote No.1,2,3 LDR sensor readings
Unknown Variables
Target's X,Y Coordinates
----
Originally I assumed that the triangle of motes was isosceles, from that point I could work out the distances between each mote. From this using the LDR readings I could then take a ratio approach and work out the distances between each mote and the target (between 2 points not 3). Using this method I could build up 6 sets of coordinates each representing the outer limits of the targets potential positions. Using these I could plot curved lines with the aim of identifying the point of intersection.
However I have realized that I cannot assume that the triangle is isosceles... As I said I am a soon to be electronic engineer not a mathematician, this problem is going into uncharted territories. I love challenges but I would appreciate a point in the right direction. Thanks for reading this, if nothing else it has been interesting learning about the differences between triangulation and trilateration!
Cheers,
Alex
Let me start by introducing myself, my name is Alex and I am in the final stages of an Electronic Engineering degree. This is not directly 'homework'. It will take me a little while to set the scene so feel free to get a cup of tea!
One of my modules (Wireless Sensor Networks) has a project that involves using 3 wireless motes and a base station. For those that have not come across this, it is simply 3 wireless sensor platforms that relay their respective data to a hub (base-station) that is connected to a computer serial port. The project was meant to be fairly straightforward; each mote has a series of embedded sensors. I was meant to pick one and then relay each motes data back to the computer and display it in a homemade GUI. I have already accomplished all of this quite successfully. (I chose to use the embedded light dependent resistors (LDR's) as my sensors.
For some brownie points (this is not in the projects spec) I thought it would be interesting if I could track the co-ordinates of a target moving around within the sensor grid. The idea being that I turn all the lights off and then send someone with a torch walking around room. The mote closest to the target would give the highest sensor reading.
The problem with this is I cannot use normal trilateration, as I do not know the distance between each mote and the target. All I have to go on is the motes LDR readings which can vary depending on the light source anywhere between readings of 3 and 1300.
Known Variables
Mote No.1,2,3 X,Y coordinates
Mote No.1,2,3 LDR sensor readings
Unknown Variables
Target's X,Y Coordinates
----
Originally I assumed that the triangle of motes was isosceles, from that point I could work out the distances between each mote. From this using the LDR readings I could then take a ratio approach and work out the distances between each mote and the target (between 2 points not 3). Using this method I could build up 6 sets of coordinates each representing the outer limits of the targets potential positions. Using these I could plot curved lines with the aim of identifying the point of intersection.
However I have realized that I cannot assume that the triangle is isosceles... As I said I am a soon to be electronic engineer not a mathematician, this problem is going into uncharted territories. I love challenges but I would appreciate a point in the right direction. Thanks for reading this, if nothing else it has been interesting learning about the differences between triangulation and trilateration!
Cheers,
Alex