- #1
dlacombe13
- 100
- 3
Hello, I am having trouble finding the direction of the resultant of this statics homework problem. The picture uploaded is exactly how it is shown in my book. The problem states:
For the forces shown, S = 3.81 kip, T = 4.73 kip, and U = 3.65 kip. Determine the resultant.
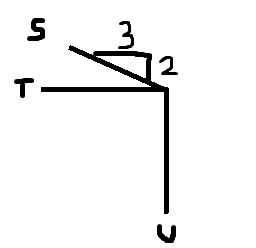
The answers to this problem are 8.05 kip @ -169 degrees.
Pythagorean Theorem (to find resultant force): C2 = A2 + B2
x-component = cos(angle)*force
y-component = sin(angle)*force
magnitude of resultant = arctan(y-component / x-component)
I have gotten the magnitude via trigonometry as such:
x-component of S = -cos(33.6901 deg) * 3.81 = -3.17011
x-component of T = -4.73
x-component of U = 0
______________________________
= -7.90011
y-component of S = +sin(33.6901 deg) * 3.81 = 2.11341
y-component of T = 0
y-component of U = -3.65
______________________________
= -1.53659
I then used the Pythagorean Theorem to find the magnitude of the resultant:
R2 = √(-7.90011)2 + (-1.53659)2 = 8.05 kip
I then took the arctan of the y-component over the x-component, which equals +11.0067 deg which is the wrong direction...
I am very lost as to why I am getting the wrong direction if I have gotten the correct magnitude. Any help?
Homework Statement
For the forces shown, S = 3.81 kip, T = 4.73 kip, and U = 3.65 kip. Determine the resultant.
The answers to this problem are 8.05 kip @ -169 degrees.
Homework Equations
Pythagorean Theorem (to find resultant force): C2 = A2 + B2
x-component = cos(angle)*force
y-component = sin(angle)*force
magnitude of resultant = arctan(y-component / x-component)
The Attempt at a Solution
I have gotten the magnitude via trigonometry as such:
x-component of S = -cos(33.6901 deg) * 3.81 = -3.17011
x-component of T = -4.73
x-component of U = 0
______________________________
= -7.90011
y-component of S = +sin(33.6901 deg) * 3.81 = 2.11341
y-component of T = 0
y-component of U = -3.65
______________________________
= -1.53659
I then used the Pythagorean Theorem to find the magnitude of the resultant:
R2 = √(-7.90011)2 + (-1.53659)2 = 8.05 kip
I then took the arctan of the y-component over the x-component, which equals +11.0067 deg which is the wrong direction...
I am very lost as to why I am getting the wrong direction if I have gotten the correct magnitude. Any help?