Trouble Understanding Hinge Axes: Ax ≠ Bx?

[annamal]

Homework Statement

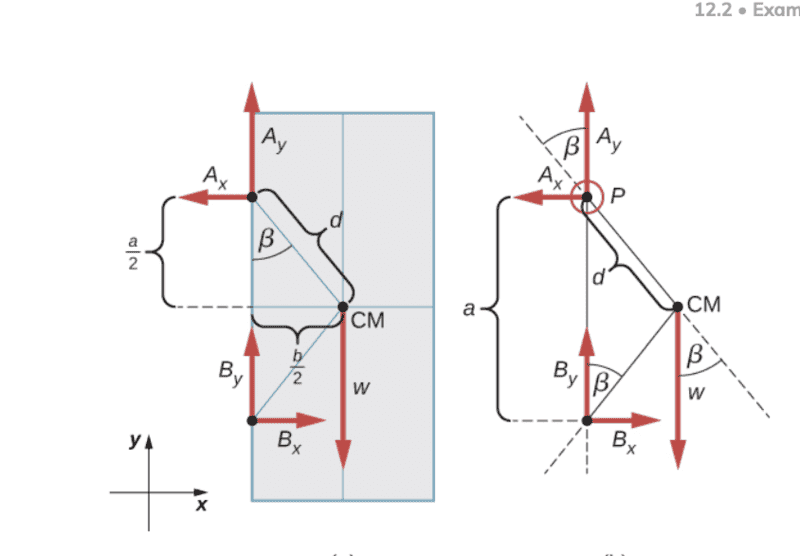
A swinging door that weighs is supported by hinges A and B so that the door can swing about a vertical axis passing through the hinges see figure. The door has a width of and the door slab has a uniform mass density. The hinges are placed symmetrically at the door’s edge in such a way that the door’s weight is evenly distributed between them. The hinges are separated by distance Find the forces on the hinges when the door rests half-open.

Relevant Equations

net torque = 0
net force = 0

I am confused by the drawing of the door with hinges A and B attached. I do not understand why -Ax = Bx. I would have thought that Ax = Bx

 

[kuruman]

There are two ways to say that the sum of the horizontal components is zero: algebraically and with reference to a vector diagram.

Algebraically, the x-comonent of the sum is the sum of the x-components. So you write $A_x+B_x=0$ which implies that if one of the them is positive the other must be negative. In other words, $-A_x=B_x$, i.e. the sum of the horizontal components is zero.

With reference to a vector diagram as the one above, the horizontal arrows are placeholders for unit vectors and their labels are the positive magnitudes of the vectors. So you write the vector equation in the horizontal direction as $A_x(-\hat x)+B_x(+\hat x)=0.$ At this point you can drop the unit vectors because the direction is preserved by the positive and negative signs. So you write $-A_x+B_x=0$ which implies that $A_x=B_x$, i.e. the magnitudes of the components are equal with the understanding that their directions, if written as vectors, are opposite.

The bottom line is that if two vectors add to zero, they must have equal magnitudes and point in opposite directions. Conversely, the only way for two vectors to add to zero is if they have equal magnitudes and point in opposite directions.

In what context did you see $-A_x=B_x$?

 

[Lnewqban]

What does resist the torque induced by W combined with b/2?

 

[nasu]

What does resist the torque induced by W combined with b/2?

The torque of Ax if you take the pivot at B. And the torque of Bx if you take the pivot at A.

 

[kuruman]

The torque of Ax if you take the pivot at B. And the torque of Bx if you take the pivot at A.

In fact, because the magnitudes of the forces are equal and their directions opposite, they form a couple. This means that they generate a counterclockwise torque of magnitude $\tau=A_xa=B_xa$ that does not depend on the choice of reference point. More generally, it's the counterclockwise couple that "resists" the clockwise torque of the weight.

 

[annamal]

There are two ways to say that the sum of the horizontal components is zero: algebraically and with reference to a vector diagram.

Algebraically, the x-comonent of the sum is the sum of the x-components. So you write $A_x+B_x=0$ which implies that if one of the them is positive the other must be negative. In other words, $-A_x=B_x$, i.e. the sum of the horizontal components is zero.

With reference to a vector diagram as the one above, the horizontal arrows are placeholders for unit vectors and their labels are the positive magnitudes of the vectors. So you write the vector equation in the horizontal direction as $A_x(-\hat x)+B_x(+\hat x)=0.$ At this point you can drop the unit vectors because the direction is preserved by the positive and negative signs. So you write $-A_x+B_x=0$ which implies that $A_x=B_x$, i.e. the magnitudes of the components are equal with the understanding that their directions, if written as vectors, are opposite.

The bottom line is that if two vectors add to zero, they must have equal magnitudes and point in opposite directions. Conversely, the only way for two vectors to add to zero is if they have equal magnitudes and point in opposite directions.

In what context did you see $-A_x=B_x$?

In the diagram attached -Ax = Bx. You're not answering my question of why -Ax = Bx. I know that Ax + Bx = 0 if that is true.

 

[Lnewqban]

In the diagram attached -Ax = Bx. You're not answering my question of why -Ax = Bx. I know that Ax + Bx = 0 if that is true.

Yes, he does.
Please, see the link he has provided.

In fact, because the magnitudes of the forces are equal and their directions opposite, they form a couple.

 

[annamal]

Yes, he does.
Please, see the link he has provided.
View attachment 299456

Yes, I see that. But I don't understand how/why they are a couple. When I open the door, I think Ax = Bx

 

[nasu]

If you ever removed a door from the hinges or put it back you should have realized that the top one is puling towards the frame. You need to tighten the screws so the door is pulled towards frame.
But if you had the door attached only at the top it will rotate with the bottom trying to get into the frame. The bottom hinge pushes against this. On the other hand, if you attach the bottom hinge first the door will try to fall away from the door frame. So you need the top hinge to pull it back.

But if your experience is not enough, the laws of physics should help. The door is in equilibrium and there are only two horizontal forces. So they have to be in opposite direction and have equal magnitude. The zero horizontal net force is a condition from equilibrium. It is not that somehow you quess that Ax=-Bx and so you ealize that the net force is zero. It is the other way around. The zero horizontal net force requires the condition above. The torques have nothing to do with it.

 

[annamal]

If you ever removed a door from the hinges or put it back you should have realized that the top one is puling towards the frame. You need to tighten the screws so the door is pulled towards frame.
But if you had the door attached only at the top it will rotate with the bottom trying to get into the frame. The bottom hinge pushes against this. On the other hand, if you attach the bottom hinge first the door will try to fall away from the door frame. So you need the top hinge to pull it back.

But if your experience is not enough, the laws of physics should help. The door is in equilibrium and there are only two horizontal forces. So they have to be in opposite direction and have equal magnitude. The zero horizontal net force is a condition from equilibrium. It is not that somehow you quess that Ax=-Bx and so you ealize that the net force is zero. It is the other way around. The zero horizontal net force requires the condition above. The torques have nothing to do with it.

Ah yes, the first paragraph clears it up in my mind. But I would never have been able to come up with that.

 

[hutchphd]

The fact that the door is not translating in x tells you they are egual and opposite. The fact that the door is not rotating (within the page) allows you to solve for their size. Done.

 

[annamal]

The fact that the door is not translating in x tells you they are egual and opposite. The fact that the door is not rotating (within the page) allows you to solve for their size. Done.

But the door is not translating in y but the forces at A and B in the y direction are not equal and opposite. Ay = By but Ax = -Bx

 

[hutchphd]

It says that they are sufficient to counteract gravity force. Same deal.

 

[nasu]

But the door is not translating in y but the forces at A and B in the y direction are not equal and opposite. Ay = By but Ax = -Bx

For the vertical direction you have three forces. The net force is the vector sum of these three. You cannot draw any conclusion about individual values of the vertical components just from this condition.

 

[Lnewqban]

Yes, I see that. But I don't understand how/why they are a couple. When I open the door, I think Ax = Bx

The combination of the weight of the door and its horizontal distance to the hinge's centerline induces those horizontal loads on the anchors of the hinges.
If those anchors were somehow elastic, we could see the top ones stretching and the bottom ones compressing.

The longer that distance, the greater is the magnitude of the opposite horizontal pair of forces.
The shorter the distance between hinges, the greater is the magnitude of the opposite horizontal pair of forces.

That is a common problem for heavy long gates.
Note how robust the anchoring of the hinges to the concrete column is in the attached picture.