Trouble understanding Newton's Third Law in Pulleys

[Abu]

Hi everyone. I found this image online that made me question a couple of things that might be a bit humiliating to ask:

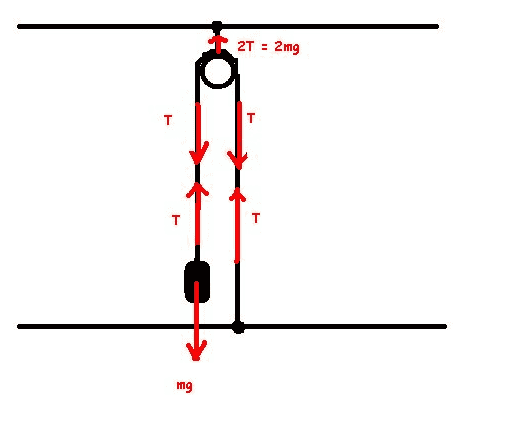
I always thought that tension is simply a pulling force, meaning that the mass is suspended because the tension force pulling the mass is equal to the weight force of the mass. But in the diagram, it also shows tension T pointing towards the mass, as if it is 'pushing' it.

What is this supposed to mean? How does this relate to Newton's Third Law?

I am guessing that, assuming the mass weighs 50 N for example, the mass pulls down on the rope with 50 Newtons (Which I am guessing is the T arrow pointing downwards towards the mass in the diagram) and due to Newtons Third Law, the rope exerts an equal and opposite pulling force of 50 N on the mass upwards.

If this is correct, I still don't understand why it looks like T is pushing down on the mass, if that makes any sense.

Thank you for your time.

 

[Doc Al]

I always thought that tension is simply a pulling force, meaning that the mass is suspended because the tension force pulling the mass is equal to the weight force of the mass. But in the diagram, it also shows tension T pointing towards the mass, as if it is 'pushing' it.

Ropes can only pull, not push. Think of "tension" as being a condition of a rope that allows it to pull at each end.

The diagram might be a bit confusing, since it shows forces on several objects. It shows the two tension forces pulling down on the pulley. And it shows the tension force pulling up on the mass. It does not show tension pushing down on the mass. (That downward force, I presume, is the object's weight.)

I am guessing that, assuming the mass weighs 50 N for example, the mass pulls down on the rope with 50 Newtons (Which I am guessing is the T arrow pointing downwards towards the mass in the diagram) and due to Newtons Third Law, the rope exerts an equal and opposite pulling force of 50 N on the mass upwards.

Careful here. An object's weight is the gravitational force that the Earth exerts on the object; per Newton's 3rd law, the object exerts an equal and opposite gravitational force on the earth. The rope does exert an upward force on the object (the tension force) and the object exerts an equal and opposite downward force back on the rope (which is not shown on the diagram).

Just to emphasize my point: The downward weight force of 50N and the upward tension force on the mass are not Newton 3rd law pairs!

 

[Abu]

Ropes can only pull, not push. Think of "tension" as being a condition of a rope that allows it to pull at each end.

The diagram might be a bit confusing, since it shows forces on several objects. It shows the two tension forces pulling down on the pulley. And it shows the tension force pulling up on the mass. It does not show tension pushing down on the mass. (That downward force, I presume, is the object's weight.)Careful here. An object's weight is the gravitational force that the Earth exerts on the object; per Newton's 3rd law, the object exerts an equal and opposite gravitational force on the earth. The rope does exert an upward force on the object (the tension force) and the object exerts an equal and opposite downward force back on the rope (which is not shown on the diagram).

Just to emphasize my point: The downward weight force of 50N and the upward tension force on the mass are not Newton 3rd law pairs!

Thank you so much for your time and reply once again!
Understanding that the weight force and the upward pulling tension force are not third law pairs cleared up a lot of my confusion, but I still have a couple more questions regarding this:

Do the two tension forces pulling down on the pulley have anything to do with Newtons third law? (It was referred to in this homework thread at post number 12 as the "third law pairs of the tension forces" https://www.physicsforums.com/threads/pulley-problem-with-two-masses.936316/#post-5916674) I understand that looking at the link might be tedious, so feel free to simply ignore it if you like.

And secondly, I am slightly confused how it would look like on the diagram where the rope exerts an upward force on the object and the object exerts a downward force back on the rope. How is it possible that the object exerts a force downwards when the rope is above it? I hope I am not overthinking this haha...

Once again, thank you for your time and patience. If my question is unclear just let me know and I won't hesitate to fix it.

 

[Chestermiller]

It is best to think of tension having a bi-directional character at each and every point along a rope under tension. If you were to cut the rope in half, for example, you would have to manually apply a force on the left half (directed to the right) in order to replace the force that the right half was exerting on it. And you would have to manually apply a force on the right half (directed to the left) in order to replace the force that the left half was exerting on it. So, at each point along a rope in tension, there is an action reaction pair acting, both sections of which are pulling the other.

 

[Doc Al]

Do the two tension forces pulling down on the pulley have anything to do with Newtons third law?

Every force has a third law pair. The "trick" is always to ask: What (A) is exerting a force on what (B)? Here it the rope (A) pulling down on the pulley (B). So the third law pair to that force is the pulley (B) pulling up on the ropes (A).

And secondly, I am slightly confused how it would look like on the diagram where the rope exerts an upward force on the object and the object exerts a downward force back on the rope. How is it possible that the object exerts a force downwards when the rope is above it? I hope I am not overthinking this haha...

Once again, if the rope (A) pulls up on the object (B), then Newton's 3rd law says that the object (B) must pull down on the rope (A).

Instead of the rope, imagine you were pulling up the object. Would you agree that if you are pulling the object up then you'd feel it pulling down on you? No way around that! There's no way for you (or the rope) to pull on anything without that thing pulling back on you (or the rope) with an equal force.

 

[Abu]

Every force has a third law pair. The "trick" is always to ask: What (A) is exerting a force on what (B)? Here it the rope (A) pulling down on the pulley (B). So the third law pair to that force is the pulley (B) pulling up on the ropes (A).Once again, if the rope (A) pulls up on the object (B), then Newton's 3rd law says that the object (B) must pull down on the rope (A).

Instead of the rope, imagine you were pulling up the object. Would you agree that if you are pulling the object up then you'd feel it pulling down on you? No way around that! There's no way for you (or the rope) to pull on anything without that thing pulling back on you (or the rope) with an equal force.

Thank you very much Doc Al and Chester, I truly appreciate the patience and effort you two have in helping me understand this concept. I'm not entirely sure how to reply to both of you in one of my own, but I am very grateful nonetheless. Sorry for the late reply, I decided to think about what has been said so far over the next day and kind of write my conclusions here so that hopefully I have a grasp on it by now.

So, imagine that we have an object that weighs 5 kilograms hanging from a cord/rope:

Since the object weighs 5 kilograms, the weight will be 49 Newtons. Similarly, the tension that the rope will experience will be 49 Newtons.
According to Newton's third law, since the rope pulls on the object with 49 Newtons (Tension), the object will also have to exert an equal and opposite force downwards on the rope of 49 Newtons. It turns out that this downwards force value is equal, numerically, to the weight value of the object. But, that does not mean that the weight and the tension are third law pairs because
A: They both act on the same object (the object) and
B: if the rope was cut, the weight would still exist however the tension would not, which means that the third law pair of the weight must be the gravitational attraction that the object has on the Earth (The Earth is so massive though, so this attraction to the object is hardly noticeable)

The reason why there is a downwards tension force acting on the pulley wheel in the first diagram (in post #1) is due to the downwards force of the box which thereby puts a downward force on the pulley itself, because the cord is obviously wrapped around the pulley wheel.

Now let's say that we have a pulley system that is not at rest like the one in the first diagram in post #1. Instead, both masses are suspended and one is heavier than the other, like this:

Lets say that:
m1 is 10 kilograms (98 Newtons)
m2 is 5 kilograms (49 Newtons)

Since the pulley is now moving, the tension that the rope experiences is not simply the weight of m2 (49 Newtons). The tension, I believe, should actually be greater because now m2 is being accelerated upwards. This means that the apparent weight of the mass should increase by: w = m(g+a).

Lets say that the tension in this rope is 65 Newtons since the system is moving. That means that m2 must also exert an equal and opposite force downwards on the rope because the rope is pulling up m2. However, these two forces do not cancel each other out because
A: The pulley system will clearly move
B: They are acting on different objects

What I mean by B is that when we draw free body diagrams for the rope and m2, they will only show the forces that influence their motion, right? It should look something like this for m2:

and something like this for the rope (that we assume is mass-less):

There is only 1 force acting on the rope because we assume that it is massless. Also, I believe that this force is not added to the weight force of the block because as I said earlier, the apparent weight of m2 should increase (I think that is decent logic, right?)

I hope I am correct in most of this. I do realize that this should be an easy topic to grasp, and that it is quite laughable at the amount of effort I've put in, but I'm determined to comprehend this fully.

If you have time, please see if my conclusion is correct. Thank you so much.

 

[Doc Al]

Your analysis of the object hanging from the rope (no acceleration) is perfect.

Since the pulley is now moving, the tension that the rope experiences is not simply the weight of m2 (49 Newtons). The tension, I believe, should actually be greater because now m2 is being accelerated upwards. This means that the apparent weight of the mass should increase by: w = m(g+a).

Yes, the tension force must be greater than the weight of m2, since m2 is accelerating upward. And it must be less than the weight of m1, since m1 is accelerating downward. Good! (What you are calling the "apparent weight" of m2 is simply the force that the rope and m2 exert on each other. That's equal to the tension in the rope.)

There is only 1 force acting on the rope because we assume that it is massless.

There is only one force shown acting on the rope because you are only considering the force that m2 exerts on it. The net force on the rope must be zero, since it is massless. (If a massless object has a net force, it will have "infinite" acceleration.)

Also, I believe that this force is not added to the weight force of the block because as I said earlier, the apparent weight of m2 should increase (I think that is decent logic, right?)

Not quite sure what you mean here about adding forces. (I would not use the term "apparent weight", since it makes things sound too mysterious.)

Keep it simple: Two forces act on m2: The weight of m2 and the tension force of the rope. And, two forces also act on m1: The weight of m1 and the tension force from the rope. (The same tension force is exerted by each end of the rope.)

As far as the rope goes, who cares since it's massless! (Usually only the forces on the two masses would appear in a diagram.)

Given that, you can solve for the unknowns: The tension in the rope and the acceleration of the masses.

I hope I am correct in most of this. I do realize that this should be an easy topic to grasp, and that it is quite laughable at the amount of effort I've put in, but I'm determined to comprehend this fully.

You're doing great! I wish every student put this much effort into understanding things.

 

[Chestermiller]

View attachment 218133

There is only 1 force acting on the rope because we assume that it is massless. Also, I believe that this force is not added to the weight force of the block because as I said earlier, the apparent weight of m2 should increase (I think that is decent logic, right?)

There is not just 1 force acting on the section of rope between the pulley and the weight m2. There is an upward tension force on the section of rope at the top, equal to the force that m2 exerts on the rope at the bottom of the section of rope. This upward tension at the top is exerted by the portion of the rope in contact with the pulley at the departure point from the pulley.