- #1
ElliottG
- 24
- 0
Hey guys
So the problem I'm having here is spans!
I know that a basis of a vector space is a linearly independent spanning set
So the linearly independent part is pretty easy...looking at whether or not vectors are linear combinations of the others (right? Or do I have to look at it by inspection and see whether or not one is a linear combination of the other? Or is that what I'm doing essentially? I'm pretty lost!), but how do I tell if a set of vectors is a span or not?
Like here's a question that I sort of understand but I don't get how to show if it's a span or not. **note this is not a homework question...it's a question on my practice test**
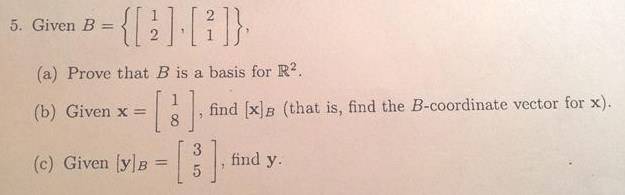
So I turn these two vectors into a matrix A, and do a row reduction to see that it does have 2 pivot positions and is indeed linearly independent, but how do I know whether or not it's a spanning set?
Does it have something to do with the funny brackets that they write?
Another thing I see is them writing stuff like this:

I mean what's the difference between writing span in front and not writing it? One is a span and the other is just a set of vectors? Blehhh :(
Edit: I think I'm sort of starting to understand it...so basically if I write this it makes sense, correct? (for the first question):

Because of this: H = span{b1, b2, ... , bp} where B = {b1, b2, ... , bp}?
Basically the span of the basis is equal to its parent vector space?
Thanks,
Elliott
So the problem I'm having here is spans!
I know that a basis of a vector space is a linearly independent spanning set
So the linearly independent part is pretty easy...looking at whether or not vectors are linear combinations of the others (right? Or do I have to look at it by inspection and see whether or not one is a linear combination of the other? Or is that what I'm doing essentially? I'm pretty lost!), but how do I tell if a set of vectors is a span or not?
Like here's a question that I sort of understand but I don't get how to show if it's a span or not. **note this is not a homework question...it's a question on my practice test**
So I turn these two vectors into a matrix A, and do a row reduction to see that it does have 2 pivot positions and is indeed linearly independent, but how do I know whether or not it's a spanning set?
Does it have something to do with the funny brackets that they write?
Another thing I see is them writing stuff like this:
I mean what's the difference between writing span in front and not writing it? One is a span and the other is just a set of vectors? Blehhh :(
Edit: I think I'm sort of starting to understand it...so basically if I write this it makes sense, correct? (for the first question):
Because of this: H = span{b1, b2, ... , bp} where B = {b1, b2, ... , bp}?
Basically the span of the basis is equal to its parent vector space?
Thanks,
Elliott
Last edited: