thatboi
- 130
- 20
Hi all,
Consider the following Green's function:
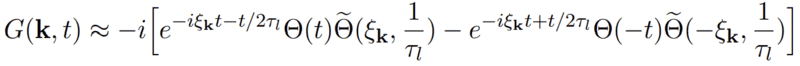
where ##\Theta(t)## is the Heaviside step function and ##\tilde{\Theta}(t)## is defined as
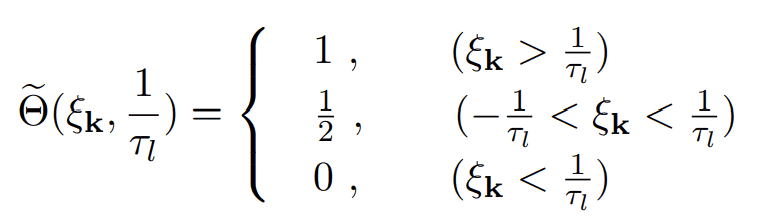
I want to understand the following calculation:
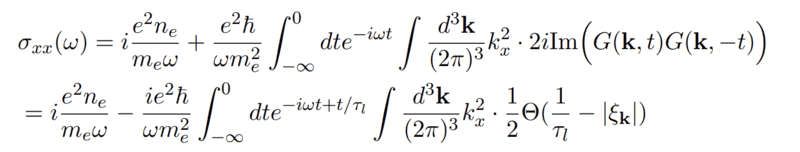
More specifically, the ##\text{Im}(G(\textbf{k},t)G(\textbf{k},-t))## from the first line to the second line. Everytime I write out the expression, the exponentials seem to just cancel and I get 0 for the imaginary part. Any assistance would be greatly appreciated.
Consider the following Green's function:
where ##\Theta(t)## is the Heaviside step function and ##\tilde{\Theta}(t)## is defined as
I want to understand the following calculation:
More specifically, the ##\text{Im}(G(\textbf{k},t)G(\textbf{k},-t))## from the first line to the second line. Everytime I write out the expression, the exponentials seem to just cancel and I get 0 for the imaginary part. Any assistance would be greatly appreciated.