- 1,191
- 683
- TL;DR Summary
- Ohm's law offset voltage
Have been busy working with a student doing a Physics prac to determine the internal resistance of an AA 1.5 V (nominal) battery. The basic formula being investigated is:
$$Vt=E_{cell}−Ir_i$$ where ##Vt## is the load (resistive only) voltage, ##E_{cell}## is the emf of the AA battery, ##I## is the circuit current and ##r_i## the internal resistance of the battery.
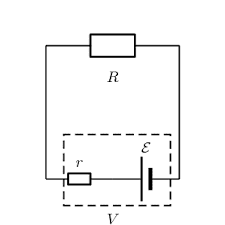 Practical problems we have had is that the terminal voltage seems to fluctuate continuously when you try to measure it. This can be mitigated somewhat by increasing the load resistance but then you start finding that the internal voltage drop is close to the limit of voltmeter resolution. R≈30Ω seems to be a reasonable value. That seems to be what is used on the "battery test" setting on my multimeter since the manual indicates an approximate current draw of 50 milli amps. (1.5 / 30).
Practical problems we have had is that the terminal voltage seems to fluctuate continuously when you try to measure it. This can be mitigated somewhat by increasing the load resistance but then you start finding that the internal voltage drop is close to the limit of voltmeter resolution. R≈30Ω seems to be a reasonable value. That seems to be what is used on the "battery test" setting on my multimeter since the manual indicates an approximate current draw of 50 milli amps. (1.5 / 30).
However the specific issue I would like to ask advice on here is that I am consistently finding discrepancies between load resistance and the quotient of (measured) load volts over (measured) amps. The regression gradient is more or less unity as expected but there is a distinct offset value of nearly 2 ohms which I cannot explain. In terms of the determination of ##r_i## this is a problem since there is wide divergence between ##\Delta V## determined as ##E_{cell}-V_t## and as ##E_{cell}-IR##.
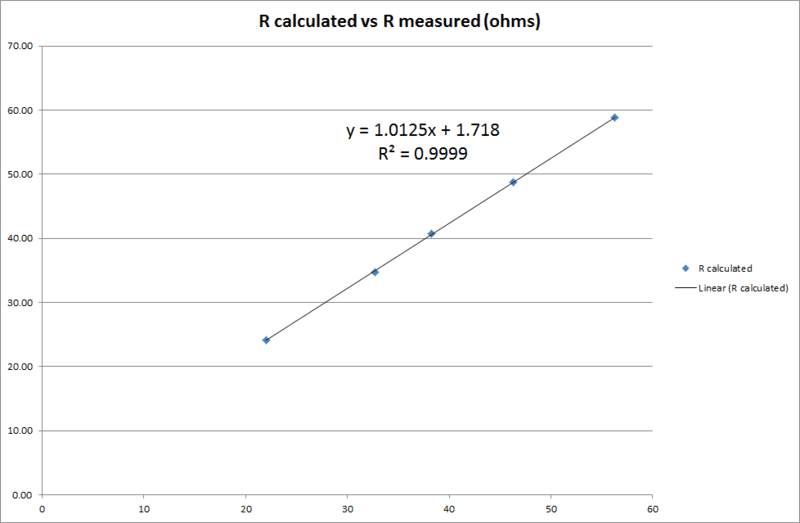
Here is my regression curve (R calculated vs R measured). Am using fixed value resistors but measuring anyway.
$$Vt=E_{cell}−Ir_i$$ where ##Vt## is the load (resistive only) voltage, ##E_{cell}## is the emf of the AA battery, ##I## is the circuit current and ##r_i## the internal resistance of the battery.
However the specific issue I would like to ask advice on here is that I am consistently finding discrepancies between load resistance and the quotient of (measured) load volts over (measured) amps. The regression gradient is more or less unity as expected but there is a distinct offset value of nearly 2 ohms which I cannot explain. In terms of the determination of ##r_i## this is a problem since there is wide divergence between ##\Delta V## determined as ##E_{cell}-V_t## and as ##E_{cell}-IR##.
Here is my regression curve (R calculated vs R measured). Am using fixed value resistors but measuring anyway.
Last edited: