Troubleshooting Nuclear Reactions: Decay, Gamma Rays & More

[Graham87]

Homework Statement

See pictures

Relevant Equations

See pictures

The problem comes with solutions. However, I dont get the 3 steps in the solutions. Why do they calculate decay for 120min in step 3? And why is only the daughter nuclide relevant and no granddaughter? There might be something lacking in my knowledge about nuclear reactions.
Also, I don't know what to use with the information "most likely gamma ray" in the question. I know it is gamma37, but what should I derive from knowing that?

Thanks!

 

[BvU]

1 Why do they calculate decay for 120min in step 3?
2 And why is only the daughter nuclide relevant and no granddaughter?
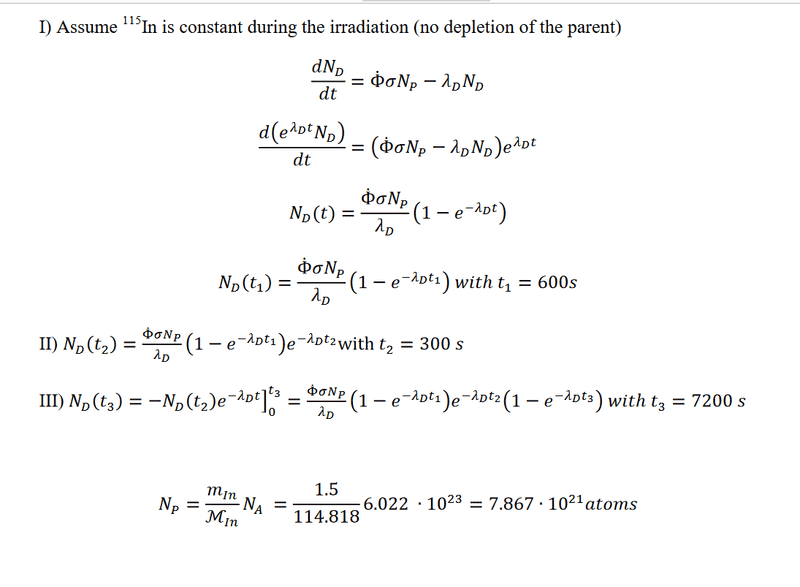
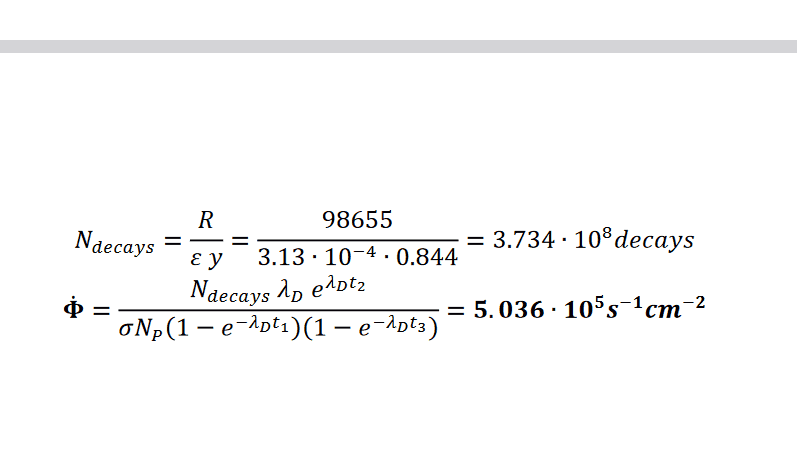
3 Also, I don't know what to use with the information "most likely gamma ray" in the question. I know it is gamma37, but what should I derive from knowing that?

1. It says so in the problem statement : they measure from 5 to 125 min
2. that last one does not decay
3. Its probability (yield) is used to divide by

And you'll learn about decay processes by doing exercises like this..

$\$

 

[Graham87]

1. It says so in the problem statement : they measure from 5 to 125 min
2. that last one does not decay
3. Its probability (yield) is used to divide by

And you'll learn about decay processes by doing exercises like this..

$\$

Regarding to calculate the fluence rate of the neutrons: how does the process of the neutrons in the reaction work? Are there neutrons decaying from the daughter particle? I cant see it. According to the reaction table the neutrons are coming from the parent particle 115(In) + n ? The daughter 116m(In) is an excited state but has no neutron decay?

So if we want to calculate the fluence rate of neutrons, why does the solution calculate the decay of the daughter, if it includes no neutrons?
Or does the daughter decay actually contribute neutrons? In that case I think I'm getting it :)

 

[BvU]

Neutrons don't play a role in the decay process that is described, only in the formation of the $^{115}$In .
The flux of incoming neutrons is determined from the amount of $^{115}$In that is found and the cross section.

$\$

 

[Graham87]

Oh, ok. I don't get step 3 - calculate the decay of the daughter for t3. What do we need that for to find the flux if the flux is from the incoming neutrons in the parent?

Thanks for the replies!

 

[BvU]

Oh, ok. I don't get step 3 - calculate the decay of the daughter for t3. What do we need that for to find the flux if the flux is from the incoming neutrons in the parent?

The way to find out how much $^{115}$In was formed in 10 minutes is to measure how many decays to Sn took place in 120 minutes.

Thanks for the replies!

You are welcome; that's what PF is for...

 

[Graham87]

The way to find out how much $^{115}$In was formed in 10 minutes is to measure how many decays to Sn took place in 120 minutes.
You are welcome; that's what PF is for...

Aha, that clears it. But how is that so? So this is because the radioactive decay is proportional to the number of daughter isotopes, which in turn is proportional to the neutron flux rate since the daughter captures neutrons from the parent?
I think I got most of it now!
Big thanks! Really appreciate it.

 

[BvU]

One more small detail:

Looking at your solution step 1 I am puzzled by step 1. I think

is wrong:
$$\begin{align*}
{{\rm d} N_D\over {\rm d} t}&= \dot\Phi\sigma N_P - \lambda N_D \\ \ \\
{{\rm d} (e^{\lambda t} N_D )\over {\rm d} t}&= \lambda e^{\lambda t} N_D + e^{\lambda t} {{\rm d} N_D\over {\rm d} t} \\ \ \\
& = \lambda e^{\lambda t} N_D + e^{\lambda t} \dot\Phi\sigma N_P - e^{\lambda t} \lambda N_D \\ \ \\
& = e^{\lambda t} \dot\Phi\sigma N_P \tag 1
\end{align*}
$$and not $\left (\dot\Phi\sigma N_P - \lambda N_D\right ) e^{\lambda t}$ as the solution states...

And then the next line in the solution follows from integrating left and right of $(1)$ from $t=0$ to $t=t_1$ :
we get $$\begin{align*}
e^{\lambda t_1} N_D(t_1) &= {\dot\Phi\sigma N_P\over \lambda} \ \left (e^{\lambda t_1} - 1\right ) \Leftrightarrow \\ \ \\
N_D(t_1) &= {\dot\Phi\sigma N_P\over \lambda} \ \left (1-e^{-\lambda t_1} \right )
\end{align*}
$$

 

[BvU]

Aha, that clears it. But how is that so? So this is because the radioactive decay is proportional to the number of daughter isotopes, which in turn is proportional to the neutron flux rate since the daughter captures neutrons from the parent?

Correction:

The way to find out how much $^{116m}$In was formed in 10 minutes is to measure how many decays to Sn took place in 120 minutes.

sorry about that. So the path is
1 flux $\rightarrow$ parents $^{116m}$In
2 parents $^{116m}_{\ \ 49}$In $\rightarrow$ $\beta, \gamma$ decay product $^{116}_{\ \ 50}$Sn

The daughter does not capture a neutron from the parent. The daughter undergoes beta decay (i.e. one neutron emits an electron and becomes a proton) yielding an excited state of the $^{116}_{\ \ 50}$Sn
This nucleus loses energy by emitting a gamma (photon)

$\$