- #1
elpermic
- 29
- 0
vectors problem, help please
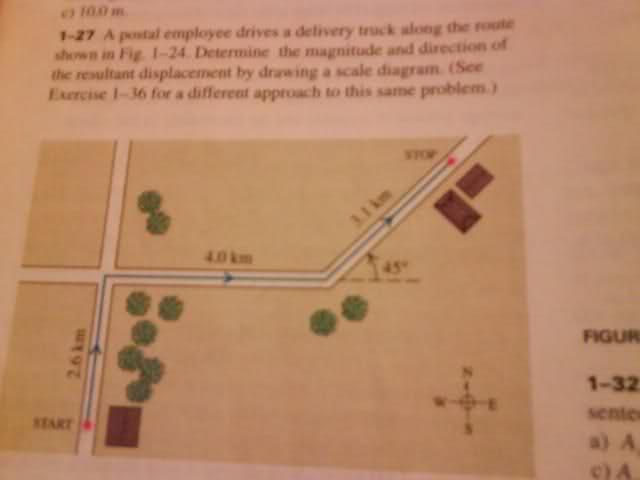
I used the pythagorem theorem on the first two vectors and named it vector x. It turned out to be 4.8km and I used vector x plus 3.1km of the other vector. I got 7.9km at 45 degrees NE. The book says it should be 7.8km at 38 degrees NE. What did I do wrong? OR is it the book>
Homework Statement
Homework Equations
The Attempt at a Solution
I used the pythagorem theorem on the first two vectors and named it vector x. It turned out to be 4.8km and I used vector x plus 3.1km of the other vector. I got 7.9km at 45 degrees NE. The book says it should be 7.8km at 38 degrees NE. What did I do wrong? OR is it the book>