True or false problem for double differentiable function

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this true or false problem,

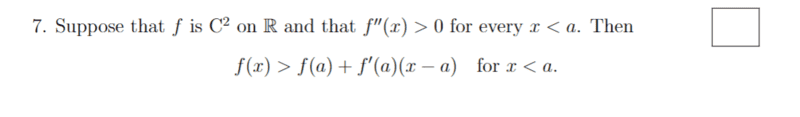
My solution is,
With rearrangement $\frac{f(x) - f(a)}{x - a} > f'(a)$ for $x < a$ since $f''(x) > 0$ implies $f'(x)) > 0$ from integration. $f'(x) > 0$ is equivalent to $f(x)$ is strictly increase which means that $\frac{f(x) - f(a)}{x - a} > f'(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x - a}$. However, I feel like I'm not showing enough steps in the proof to show for sure that the answer is True.

Does anybody else agree and know what more I should include?

Thanks!

 

[Orodruin]

since $f''(x) > 0$ implies $f'(x)) > 0$ from integration

Counter example:
$$
f(x) = x(x - 1)
$$
This leads to $f''(x)= 2 > 0$ and $f'(x) = 2x - 1$, which is negative for $x < 1/2$.

 

[nuuskur]

Second derivative positive implies $f$ is convex for $x<a$. Take anything that is convex and decreasing for (some) $x<a$ as counterexample to your claim of $f'(x)>0$.

As for the initial claim, think again of convexity. The slope at $x=a$ must be as large as it gets as $x\to a-$. Moving to the left necessarily decreases the slope.

To illustrate, let $f(x)=x^2$ and $a=1$. The slope at $a=1$ is $2$, whereas if $x=1-\delta$, then
<br /> \frac{1-(1-\delta)^2}{\delta} = 2-\delta&lt;2.<br />

Apply this concept in the general case.

 

[FactChecker]

Counter example:
$$
f(x) = x(x - 1)
$$
This leads to $f''(x)= 2 > 0$ and $f'(x) = 2x - 1$, which is negative for $x < 1/2$.

I don't think that is a counter example. $f'(x)(x-1/2)$ is positive, so $f(x) > f(1/2) + f'(1/2)(x-1/2) = -1/4$ for $x < 1/2$

 

[pasmith]

I don't think that is a counter example. $f'(x)(x-1/2)$ is positive, so $f(x) > f(1/2) + f'(1/2)(x-1/2) = -1/4$ for $x < 1/2$
View attachment 345170

It i a counter example to the assertion f&#039;&#039;(x) &gt; 0 \Rightarrow f(x) &gt; 0.

 

[mathwonk]

the thing that puzzled me is that the original statement was true in all my examples (since the hypothesis implies the left part of the curve lies above its tangent line,) but the rearranged one was not. Then I finally noticed you had divided your inequality by the negative number (x-a), which should have changed its direction.

 

[Orodruin]

I don't think that is a counter example. $f'(x)(x-1/2)$ is positive, so $f(x) > f(1/2) + f'(1/2)(x-1/2) = -1/4$ for $x < 1/2$
View attachment 345170

Not to the problem statement, to the OP’s assertion that I quoted.

 

[FactChecker]

Not to the problem statement, to the OP’s assertion that I quoted.

Sorry. I missed that point. I stand corrected.