Truss analysis- why does it not work in this case?

[Urmi Roy]

Homework Statement

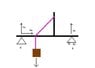
Solve for the support reactions (at A and B) in the figure given.
(the pink thing is a cable and there's an arbitrary weight hung at the end of the cable).

Homework Equations

sum of forces in y direction=0
sum of forces in x direction=0
Sum of moments =0

The Attempt at a Solution

I tried solving this using the method of joints in TRUSSES. However, consider point A (JOINT A). Here, there's the vertical component of support reaction and no other vertical force to cancel this, so joint A is not in equilibrium.
Why does the method of joints not work in this case?

My professor told me that Truss analysis doesn't work in structures that are not 2 force members...however, I find many contradictions to this.

Please give me a solution to this problem.

 

[Urmi Roy]

Please help...this is a critical point I need to understand...

 

[PhanthomJay]

Your professor is correct..this is a frame, not a truss. the horizontal member is not a 2 force member, it can take shear at the joint which balances the support reaction force. Solve for the vert reactions at A and B by summing moments of the applied and reaction forces about a point. You can solve for the horiz force at the support A by summing forces in the x direction.

 

[Urmi Roy]

Okay, so I googled this: "A truss is a structure made up of straight members which are connected at the joints, and having the joints at the ends of the members. Trusses are used to support roofs, bridges and other structures. The basic structure is triangular, or trapezoidal.

Frames are structures often composed of pin-connecting multi-force members ( i.e. subjected to three or more forces). Unlike trusses, they are not necessarily rigid e.g. linked mechanisms."...

But i can't see what difference it makes in the mechanical analysis of trusses and frames and what is the idea with two force members...why does the truss have to be a two force member?

 

[Pyrrhus]

Forces are applied at joints in a truss. Can you tell which forces violate such a statement here?

 

[Urmi Roy]

I guess at point A, there is really no joint, so the support force at A is one such force...now you're saying that in trusses, there are joints...whereas in frames, there are pin connections? But again, how does this affect the mathematical analysis?? Pin connections are treated pretty much the same way as joints...And what does it have to do with a truss being 2 force member??

 

[PhanthomJay]

I guess at point A, there is really no joint, so the support force at A is one such force...now you're saying that in trusses, there are joints...whereas in frames, there are pin connections? But again, how does this affect the mathematical analysis?? Pin connections are treated pretty much the same way as joints...And what does it have to do with a truss being 2 force member??

Your definition of a truss is incomplete in that trusses are made up of straight, pinned joint, members connected in such a way as to form a series of interconnecting triangles with loads assumed applied at joints only.

A 2-force member is a member subjected to 2 forces only (one at each end) with no forces in between. From equilibrium consisderations, these 2 forces must be equal and opposite and in line with each other (colinear), with the result that 2 force members only take axial tension or compression loads, no shear forces and no bending stresses (moments). The horizontal member in your problem has more than 2 forces acting on it, so this is not a 2-force member; it has shear and bending stresses in it.

 

[Urmi Roy]

Your definition of a truss is incomplete in that trusses are made up of straight, pinned joint, members connected in such a way as to form a series of interconnecting triangles with loads assumed applied at joints only.

Okay, now stressing on the fact that in a truss, the members are pin jointed--- this is true in frames also...the main difference I see between trusses and frames is that in trusses, the loads are applied only at the joints, whereas in frames, this need not be true...in frames also , there might be interconnected triangles...so what exactly is the main difference?

A 2-force member is a member subjected to 2 forces only (one at each end) with no forces in between. ...

I get this, but what does it have to do with truss analysis? The question is why can't we apply the methods of truss analysis to structures that are not 2-force members.

 

[PhanthomJay]

Okay, now stressing on the fact that in a truss, the members are pin jointed--- this is true in frames also...

in some frames, yes, but not all frames

the main difference I see between trusses and frames is that in trusses, the loads are applied only at the joints, whereas in frames, this need not be true...in frames also , there might be interconnected triangles...so what exactly is the main difference?

In trusses, all loads are assumed applied at joints, and all members ...not just some of them...are interconnected to form triangles...

I get this, but what does it have to do with truss analysis? The question is why can't we apply the methods of truss analysis to structures that are not 2-force members.

In truss analysis, all members have tension or compression loads (or no loads) that act axially along the member's long axis ; in frames, loads can support compression or tension or shear (perpendicular to the long axis) stresses, and bending stresses from bending moments as well (I think I said that already, so this probably doesn't help you). In your example, the horizontal member from A to the first joint (where the cable is attached) does not interconnect with another member to form a triangle. When you look at a free body diagram of joint A, the vertical support reaction at A is balnced in the member by an equal but opposite shear force in the member, introducing bending stresses further in that member as well. It is not a 2 force member.

 

[Urmi Roy]

in some frames, yes, but not all frames In trusses, all loads are assumed applied at joints, and all members ...not just some of them...are interconnected to form triangles... In truss analysis, all members have tension or compression loads (or no loads) that act axially along the member's long axis ; in frames, loads can support compression or tension or shear (perpendicular to the long axis) stresses, and bending stresses from bending moments as well...

So the main issue is that in trusses, its only tension/compression along the axis of each member and while we apply the method of joints, our analysis doesn't or rather 'cannot' include shear forces, since shear forces are internal forces and we can't include them in analyzing the external mechanical equilibrium of a body?

Is that okay?

 

[PhanthomJay]

So the main issue is that in trusses, its only tension/compression along the axis of each member and while we apply the method of joints, our analysis doesn't or rather 'cannot' include shear forces, since shear forces are internal forces and we can't include them in analyzing the external mechanical equilibrium of a body?

Is that okay?

Well, not quite. It is true that ideal truss members only take compression or tension. but when you apply the method of joints, there is no perpendicular internal shear force in the member..for straight pinned 2 force members, they don't exist perpendicular to the member. When you are looking at the system as a whole and trying to find the support reactions first (which is a good idea), then you look at external forces only (including the support reactions, and applied loads, which in your example is the weight) and use the 3 equations for equilibrium (sum of forces in each direction and sum of moments about any point = 0)

 

[Urmi Roy]

Well, not quite. It is true that ideal truss members only take compression or tension. but when you apply the method of joints, there is no perpendicular internal shear force in the member..for straight pinned 2 force members, they don't exist perpendicular to the member. When you are looking at the system as a whole and trying to find the support reactions first (which is a good idea), then you look at external forces only (including the support reactions, and applied loads, which in your example is the weight) and use the 3 equations for equilibrium (sum of forces in each direction and sum of moments about any point = 0)

Right...and these perpendicular forces may exist in members constituting a frame, and, which are not necessarily two-force members...?

 

[PhanthomJay]

Right...and these perpendicular forces may exist in members constituting a frame,

correct, internal shear forces

and, which are not necessarily two-force members...?

If a straight member has shear in it perpendicular to the longitudinal axis, it is not a 2 force member

 

[Urmi Roy]

Thanks :-) Your posts cleared it all up :-)