bugatti79
- 786
- 4
- TL;DR Summary
- establish connection between the 2 rotating quadrants
Hello All,
I struggled to find a closed form solution connecting the 2 quadrants via the angles alpha and beta. I filled the schematic with right angle triangles hoping to find a connection but to no avail.
In the end, I decided to create a polynomial function of beta in terms of alpha as I know the coordinates of the vertices. Could someone confirm that a closed form solution is not possible? Is there any way I could use a custom analytic function of beta in terms of alpha? Thanks!


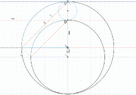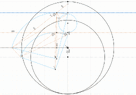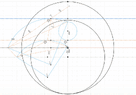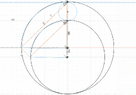

I struggled to find a closed form solution connecting the 2 quadrants via the angles alpha and beta. I filled the schematic with right angle triangles hoping to find a connection but to no avail.
In the end, I decided to create a polynomial function of beta in terms of alpha as I know the coordinates of the vertices. Could someone confirm that a closed form solution is not possible? Is there any way I could use a custom analytic function of beta in terms of alpha? Thanks!


Last edited by a moderator: