Trying to reproduce curves with angle of CMB anisotropies

[fab13]

I am looking for a way to get, by a simple numerical computation, the 3 curves on the following figure:

For this, I don't know what considering as abcissa (comoving distance ?, i.e

$D_{comoving} = R(t)r$

with $R(t)$ scale factor and $r$ the coordinate which appears into FLRW metric).

Previously, I found a little project about the trajectory of light geodesics in an expanding universe; here below a figure illustrating the expected results with FLRW metric:

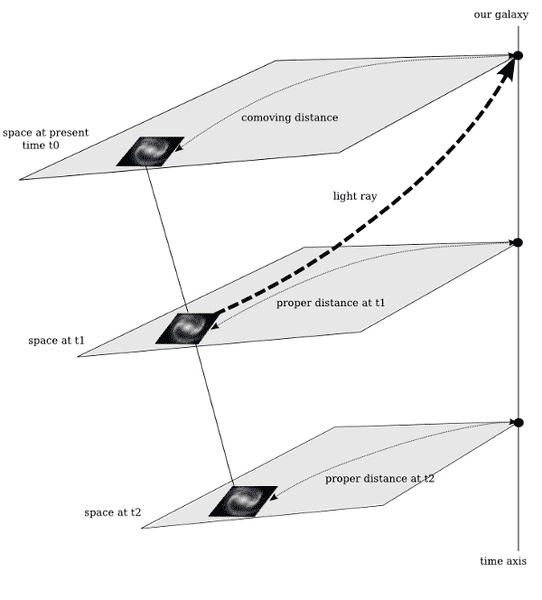
As you can see, the curve of light is bended since $\Lambda\text{CDM}$ current model produces acceleration of expansion, so light has more and more difficulties to reach our galaxy.

In a first version of this project, I have computed a light geodesic in Einstein-de-Sitter universe : so in this case, the distance between the 2 galaxies (emitting and our galaxy) which is equal to :

$D_{{\varphi}}=\text{Distance}_{init}\,\bigg[\frac{3\,H_{0}}{2c}\,ct\bigg]^{2/3}$

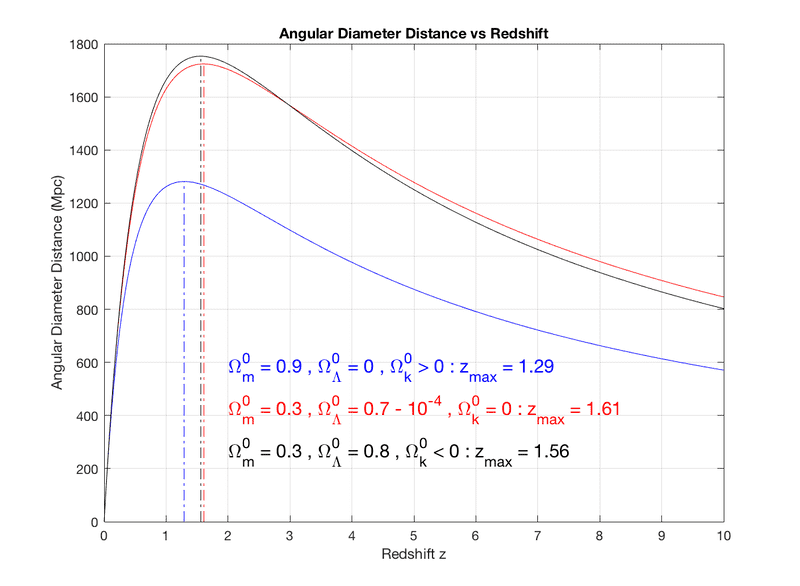
I did also a simple computation on the angular diameter distance versus the redshift. I get this figure which is the expected results for the 3 models (k=-1,0,1) :

I would have thought that angle of anistropies was constant during its travel : that is not the case on the first figures at the top of post, which illustrates a bending, producing then a different angle between the initial emission and the final reception by our eyes : **is it actually right ?**

I think my main issue, to produce this first figure, is to know what I have got to take as abscissa ? the comoving distance, the proper distance, the angular diameter distance ?

Firstly, I believed that I should take the comoving distance but I don't know how to make converge 2 light rays (extremities of one anisotropy) in oberver eyes.

Any help is welcome to reproduce the 3 curves on the first figure of this post : these curves illustrate very well the notion of smaller/bigger value of apparent anisotropies as a function of curvature parameter.

 

[kimbyd]

I don't have a really substantive answer right now, but one important point is that the pictures at the top are not likely to be from any sort of real calculation. Rather they're a heuristic device. If you had a two-dimensional surface that was flat, positively-curved, or negatively curved, then triangles on those surfaces would look much like the three displayed above. For instance, the Earth is positively-curved (akin to a closed universe), so if you draw a large enough triangle on the surface of the Earth, with the edges of the triangle being geodesics (great circles for the Earth), then it will look much like the "closed universe" triangle when viewed from space.