Kashmir
- 466
- 74
I've a disc which can rotate freely about two perpendicular axis (fixed to the body)
If I simultaneous try to rotate it about the two axis, what will happen?
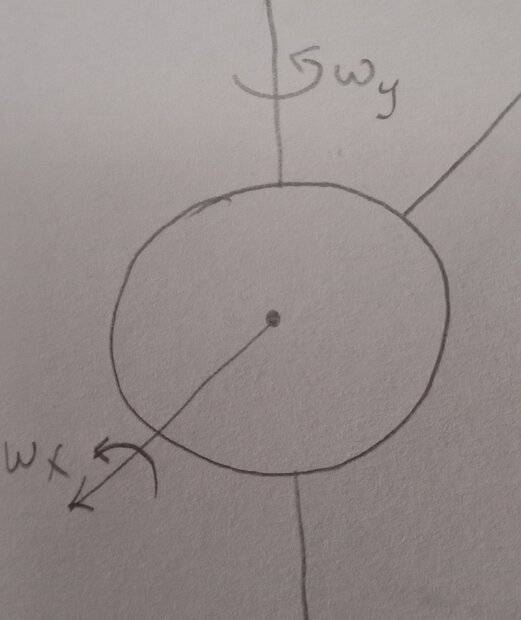
If I simultaneous try to rotate it about the two axis, what will happen?
Last edited: