- #1
avery
- 24
- 0
I am trying to understand the following equation:
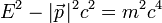
what is P?
what is P?
thank you NabeshinNabeshin said:
This equation, also known as the relativistic energy-momentum relation, represents the relationship between energy (E), momentum (p), and mass (m) in the theory of special relativity. It is used to calculate the energy and momentum of an object moving at high speeds, close to the speed of light.
The equation is derived from the fundamental principles of special relativity, which include the constancy of the speed of light and the equivalence of mass and energy. It can also be derived from the Lorentz transformations, which describe how measurements of space and time change between different reference frames.
This equation is important because it allows us to understand the behavior of objects moving at high speeds, which cannot be accurately described by classical mechanics. It also illustrates the interplay between mass, energy, and momentum, and how they are all interconnected in the theory of special relativity.
This equation is used in a variety of fields, including particle physics, astrophysics, and engineering. It is used to calculate the energy and momentum of particles in particle accelerators, to understand the behavior of objects in space, and to design spacecraft and other high-speed technologies.
Yes, this equation can be simplified for specific scenarios, such as objects traveling at a constant velocity or in a specific direction. It can also be generalized for different types of mass and energy, such as for photons (massless particles) or for systems with multiple particles. However, it is important to note that this equation is only applicable in the context of special relativity and does not hold true in classical mechanics.