- #1
Saints-94
- 63
- 1
I have ran an FEA simulation on a lever to work out the stress on the part. I have now started doing some hand calculations to validate the software results and am struggling to get the values to match up. I am unsure whether my calculations are wrong, or whether the software is incorrect.
The part is a metal tube (below), with a 25.3mm diameter and 2mm wall thickness.
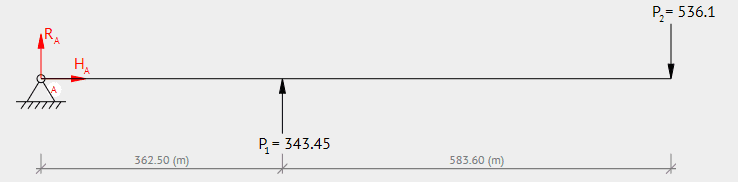
I know that;
Stress = My / I
I have worked my bending moment out as
M(x1) = + RA*(x1) - MA
M1(0) = + 192.65*(0) - 382703.59 = -382703.59 (N*m)
M1(362.50) = + 192.65*(362.50) - 382703.59 = -312867.96 (N*m)
Y= D/2
=12.65mm = 0.01265m
I = (pi * D^4) / 64
= (pi/64) * (0.0253^4 - 0.0233^4)
The answer I have calculated is 7.05 x 10^11 Nm2
and FEA analysis = 2.1 x 10^8 Nm2
Please come someone confirm whether my hand calcs are correct or not?
The part is a metal tube (below), with a 25.3mm diameter and 2mm wall thickness.
I know that;
Stress = My / I
I have worked my bending moment out as
M(x1) = + RA*(x1) - MA
M1(0) = + 192.65*(0) - 382703.59 = -382703.59 (N*m)
M1(362.50) = + 192.65*(362.50) - 382703.59 = -312867.96 (N*m)
Y= D/2
=12.65mm = 0.01265m
I = (pi * D^4) / 64
= (pi/64) * (0.0253^4 - 0.0233^4)
The answer I have calculated is 7.05 x 10^11 Nm2
and FEA analysis = 2.1 x 10^8 Nm2
Please come someone confirm whether my hand calcs are correct or not?
